Question 1129186: Use any method to solve the nonlinear system. (Order your answers from smallest to largest x, then from smallest to largest y. If there is no solution, enter NO SOLUTION.)
x^2 + y^2= 6
xy= 1
Can someone help, I use the method of and my final answers, which keeps being tagged incorrect, have been:
x: 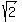 -1, y: -1, y: 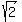 +1 +1
x: - 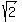 +1, y: - +1, y: - 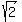 -1 -1
x: 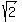 +1, y: +1, y: 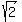 -1 -1
x: - 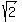 -1, y: - -1, y: - 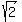 +1 +1
Am I just incorrectly ordering them from smallest to least or are the entire answers wrong?
Here is some of my work:
For x^2 + y^2= 6, substitute x with 1/y.
(1/y)^2 +y^2= 6;
For xy=1, substitute y with 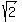 +1 +1
x(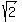 +1 )=1 +1 )=1
x= 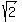 -1 -1
For xy=1, substitute y with 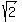 -1 -1
x(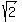 -1 )=1 -1 )=1
x= 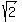 +1 +1
For xy=1, substitute y with -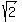 +1 +1
x(-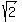 +1 )=1 +1 )=1
x= -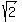 -1 -1
Found 3 solutions by josgarithmetic, MathLover1, ikleyn:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Your solutions are correct. I mean, you have the set of four solutions correctly.
Their ordering instruction is presented in a very strange way.
You can order the pairs looking in x first, but then you have no choice to order in y.
It forces me to think that they ask you to make your ordering TWICE:
- first time by ordering 4 pairs looking in x;
- and the second time by ordering the same 4 pairs looking in y.
In any way, it is not a Mathematical way to formulate an assignment.
----------------
The two other tutors presented the solutions to the roots, although nobody asked them to do it - you just have the solutions correctly.
The post by @josgarithmetic is the way to NOWHERE, as it often happens with him - so you can simply IGNORE his post, for your safety.
|
|
|