SOLUTION: Solve for x in the given interval. sec x=(2sqrt3)/3 ((3pi)/2)≤x ≤(2pi)

First we take the reciprocals of both sides, using the

fact that the reciprocal of the secant is the cosine:







Rationalize the denominator on the right side:



















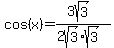
This is positive, and the cosine is positive in QI and QIV



From the unit circle, we get the first quadrant answer as 30°

or 



The interval  is Q4,



So to get the angle in Q4, we subtract from .







Answer: 



Edwin