SOLUTION: Let A and Between sit around table with twelve other person. What is probability that exactly three person between them?

This problem is about "circular permutations", so we can assume that all the chairs around the table are numbered sequentially 

from 1 to 2+12 = 14  inclusively and that the person A is sitting on the chair #1.


Then person B can occupy any of the rest 13 chairs, but the chairs #5 and #11 are favorable.


So, the probability under the question is the ratio 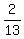 .     ANSWER

This problem is about "circular permutations", so we can assume that all the chairs around the table are numbered sequentially 

from 1 to 2+12 = 14  inclusively and that the person A is sitting on the chair #1.


Then the person B is sitting EITHER on the chair #5  OR  on the chair #11.


    In the first case, we have 12*11*10 ways to place first 3 of remaining 12 persons on the chairs #2, #3 and #4,  
    and we have  9*8*7*6*5*4*3*2*1 ways to place the rest of 12 people on the remaining chairs.

    It gives us  12! different ways.



    In the second case we have THE SAME NUMBER of different ways.



    Hence, in all, there are 2*12! different placements/arrangements that satisfy the condition (favorable arrangements).


    The total number of circular arrangements of 14 persons is 13!, as it is well known.


    So, the probability under the question is the ratio 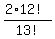 , which is equal to  .


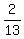    We got the same answer.