Question 1128236: According to the conjugate root theorem, if a polynomial with rational coefficients has -1+√6; -2√2; -3-i as roots, what are the other roots?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52864)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are TWO conjugate root theorems:
One (the most widely known) conjugate root theorems says:
If a polynomial with real coefficients has a root a+bi with real "a" and "b", and i = 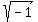 ,
then it has the root a-bi, too.
The other conjugate root theorem says:
If a polynomial with rational coefficients has a root ,
then it has the root a-bi, too.
The other conjugate root theorem says:
If a polynomial with rational coefficients has a root 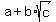 with rational "a" and "b",
then it has the root with rational "a" and "b",
then it has the root 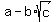 , too.
By applying one and another conjugate root theorem to the given problem, we obtain that
the root , too.
By applying one and another conjugate root theorem to the given problem, we obtain that
the root 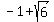 goes in pair with the root goes in pair with the root 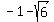 ;
the root ;
the root 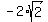 goes in pair with the root goes in pair with the root  ;
the root ;
the root 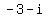 goes in pair with the root goes in pair with the root 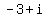 .
So, the polynomial has, in total, 6 (six; SIX) listed roots. .
So, the polynomial has, in total, 6 (six; SIX) listed roots.
Solved, answered and completed.
|
|
|