SOLUTION: An investment firm recommends that a client invest in bonds rated​ AAA, A, and B. The average yield on AAA bonds is 6​%, on A bonds 7​%, and on B bonds 10​%

Algebra ->  Coordinate Systems and Linear Equations -> SOLUTION: An investment firm recommends that a client invest in bonds rated​ AAA, A, and B. The average yield on AAA bonds is 6​%, on A bonds 7​%, and on B bonds 10​%      Log On


   

Question 1128089: An investment firm recommends that a client invest in bonds rated​ AAA, A, and B. The average yield on AAA bonds is 6​%, on A bonds 7​%, and on B bonds 10​%. The client wants to invest twice as much in AAA bonds as in B bonds. How much should be invested in each type of bond if the total investment is ​$21,000​, and the investor wants an annual return of ​$1,520 on the three investments.The client should invest ​$____ in AAA​ bonds, ​$____ in A​ bonds, and ​$____ in B bonds.
Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let x = how much is invested in B bonds, in dollars.

Then the amount invested at AAA bonds is 2x, 

while the amount invested in A bonds is the rest, (21000-x - 2x) = (21000-3x) dollars.


Then your "investment" equation is


    0.06*(2x) + 0.07*(21000-3x) + 0.10*x = 1520.


Simplify and solve for x:


    0.12x + 0.07*21000 - 0.21x + 0.10x = 1520

    0.01x = 1520 - 0.07*21000

    0.01x = 50  ====>  x = 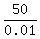50%2F0.01 = 5000.


Answer.  $5000 in B bonds;   $10000 in AAA bonds;  and the rest  (21000-5000-10000) = 6000 dollars in A bonds.


Check.   0.06*10000 + 0.07*6000 + 0.10*5000 = 1520 dollars.   ! Correct !

Solved.