Question 1128085: At 7 a.m. Joe starts jogging at 6 mi/h. At 7:10 a.m. Ken starts off after him. How fast must Ken run in order to overtake him at 7:30 A.M?
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39625)   (Show Source):
Answer by ikleyn(52852)  (Show Source):
You can put this solution on YOUR website! .
At 7 a.m. Joe starts jogging at 6 mi/h. At 7:10 a.m. Ken starts off after him. How fast must Ken run in order to overtake him at 7:30 A.M?
~~~~~~~~~~~~~~~~~~~~~
There is no need to explain you that 10 minutes from 7:00 am to 7:10 am are exactly  of an hour.
Also, there is no need to explain you that 20 minutes from 7:10 am to 7:30 am are exactly  of an hour.
From 7:00 am to 7:10 am Joe jogged 6 mi/h * of an hour = 1 mile.
So, at 7:10 am Joe is 1 mile ahead from starting point and from Ken.
Let "x" be the rate Ken is jogging. This value is now unknown - we should find it.
Now, their relative speed is (x-6) miles per hour.
(x-6) miles per hour is the rate of decreasing the distance between them, which originally was 1 miles.
Ken shoud catch up Joe in 20 minutes = of an hour; therefore the relative speed must be 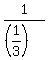 = 3 miles per hour.
In other words, the equation must hold
x - 6 = 3,
which gives you THE ANSWER x = 6 + 3 = 9 miles per hour.
The solution is COMPLETED. The problem is SOLVED.
----------------
For your safety, IGNORE WRITING bY @josgarithmetic, since it is T O T A L L Y W R O N G.
----------------
Regarding @josgarithmetic, this person is VERY well known (or better to say, very badly known, unfortunately) in this forum,
for his inability to solve problems correctly and to make calculations accurately.
So be very careful when you obtain "solutions" from him.
In half of all cases (if not at most cases) they are wrong.
Do not trust him and always wait for reaction of other tutors.
In the normal school environment he would be fired in the second day.
I think about thousands of visitors and students who do understand almost nothing in Math and who were misguided
by his false and wrong quasi- and pseudo-"solutions".
People, be careful about @josgarithmetic ! ! !
Answer by MathTherapy(10555)  (Show Source):
|
|
|
