Question 1128079: f(x)={(1,4),(2,2),(8,3),(3,3),(-7,1),(8,-1)}
I need to answer these questions about the relation above.
a) Determine the value of f(3)
b) Solve f(x) = 2
c) Determine f^-1(4)
d) Determine if f^-1 is a function.
e) What is the domain and range?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
f(x)={(1,4),(2,2),(8,3),(3,3),(-7,1),(8,-1)}
The relation is not a function.
Since  produces produces  and and , the relation is , the relation is  a function. a function.
a) Determine the value of 
from given points you see that 
b) Solve 
from given points you see that  -> ->
c) Determine 
The inverse of a function differs from the function in that all the x-coordinates and y-coordinates have been switched. That is, if ( , , ) is a point on the graph of the function, then ( ) is a point on the graph of the function, then ( , , ) is a point on the graph of the inverse function. ) is a point on the graph of the inverse function.
so, since we have no point where  there is no inverse there is no inverse 
d) Determine if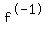 is a function. is a function.
if f(x)={(1,4),(2,2),(8,3),(3,3),(-7,1),(8,-1)}, inverse will be
f^-1 (x)={(4,1),(2,2),(3,8),(3,3),(1,-7),(-1,8)}
since  produces produces  and and  , the relation is , the relation is  a function a function
e) What is the domain and range?
the domain and range of given relation:
domain={-7,-1,1,2,3,8}
range={-1,1,2,3,4}
the domain and range of inverse:
domain={-1,1,2,3,4}
range={-7,-1,1,2,3,8}
|
|
|