Question 1128014: A magazine company had a profit of $98,000 per year when it had 32,000 subscribers. When it obtained 38,000 subscribers, it had a profit of $117,500. Assume that the profit P is a linear function of the number of subscribers s.
(a) Find the function P.
P(s) =
(b) What will the profit be if the company obtains 50,000 subscribers?
$
(c) What is the number of subscribers needed to break even? (Round to the next highest subscriber.)
subscribers
Found 2 solutions by addingup, MathTherapy:
Answer by addingup(3677)   (Show Source): (Show Source):
You can put this solution on YOUR website! The problem gives us two ordered pairs, (32,000 , $98,000) and (38,000 , $121,500
With this information we can establish the folowing equations:
m = (y2 - y1)/(x2 - x1)
y = mx + b
Slope m = (P2 - P1)/(S2 - S1) = ($117,500 - $98,000)/(38,000 - 32,000) = $19,500 / 6,000 = $47 / 12
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A magazine company had a profit of $98,000 per year when it had 32,000 subscribers. When it obtained 38,000 subscribers, it had a profit of $117,500. Assume that the profit P is a linear function of the number of subscribers s.
(a) Find the function P.
P(s) =
(b) What will the profit be if the company obtains 50,000 subscribers?
$
(c) What is the number of subscribers needed to break even? (Round to the next highest subscriber.)
subscribers
For the function, P(s), the slope is NOT 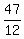 . .
Just thought I'd let you know. Everything will be wrong if you go along with that WRONG slope.
|
|
|