.
From the condition, you have these two equations
v*(t+1.5) = 2700 (1) ("the first plane flies 1.5 hours longer than the the second plane and travels 2700 miles")
v*t = 2025 (2) ("the second travels 2025 miles at the same rate")
where v is their common rate and t is flying time for the second plane.
Divide equation (1) by equation (2) (both sides. You will get
= 
= 
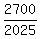3*(t+1.5) = 4t
3t + 4.5 = 4t
t = 4.5 hours.
Answer. The second plane was flying for 4.5 hours; the first plane was flying for 4.5 + 1.5 = 6 hours.
Solved.
-------------------
This solution can be presented in wording form, with minimal use of equations.
The ratio of distances is 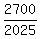= ; hence, the ratio of times is , too
(since the rate is the same for both planes).
Hence, first plane traveled 4x hours, while the second plane traveled 3x hours.
We are given that 4x - 3x is 1.5 hours; hence x = 1.5 hours.
Then the first plane was flying 4*1.5= 6 hours, while the second plane was flying 3*1.5 = 4.5 hours.
You got the same answer.
Solved for the second time.
