Question 112794: use the ac test to determine if trinomial is factored. find values of m and n.
x^2-3x+7
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! I think you meant to say "use the ac test to determine if the trinomial is factorable," and I'm presuming the m and n you are referring to are the m and n in the following:

First the AC method. A and C refer to the coefficients on the equation in standard form, namely: 
The first step of the AC method is to determine the product 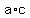 . In this case it is . In this case it is 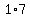 . .
The second step of the AC method is to list the possible factor pairs of the product 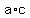 . In this case, 7 is a prime number so the only factor pairs that exist are (1,7) and (-1,-7). . In this case, 7 is a prime number so the only factor pairs that exist are (1,7) and (-1,-7).
The third step is to find a factor pair that adds up to b or -3 in this problem. But there is no such pair because 1 + 7 = 8 and (-1) + (-7) = -8. Therefore, the trinomial is not factorable.
Since the trinomial is not factorable, we are left with completing the square to find values for m and n in  . .
Completeing the square:
Step 1:
 . Begin with the original trinomial set equal to zero. . Begin with the original trinomial set equal to zero.
 . Add the negative of the constant term to both sides. (if the coefficient on the . Add the negative of the constant term to both sides. (if the coefficient on the  term were other than 1, you would have the preliminary step of dividing both sides by that coefficient) term were other than 1, you would have the preliminary step of dividing both sides by that coefficient)
 . Take the coefficient on the x term, divide by 2 and then square the result and add that result to both sides of the equation. . Take the coefficient on the x term, divide by 2 and then square the result and add that result to both sides of the equation.
 . And simplify the right side. . And simplify the right side.
Now the left side of the equation is a perfect square that can be factored.


But we have a problem because 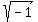 doesn't exist. So we define the imaginary number doesn't exist. So we define the imaginary number  such that such that  . Now we can write: . Now we can write:
 , So, , So,
 or or  , which is to say: , which is to say:
 or or  . And now we can say that: . And now we can say that:
 and finally, and finally,
 and and 
Now we still have to check the answer:
Is this statement true? 
Apply the FOIL method to the left side:
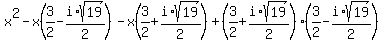
 Remembering that Remembering that 
Now collect terms and watch all of those pesky radicals go away:
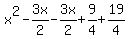
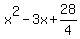
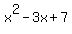
And the answer checks.
Hope this helps.
John
|
|
|