Question 1127892: Use a calculator to graph the function. Then, using the graph, give three points on the graph of the inverse with the y-coordinates given.
f(x) = x^3 + x − 4, y = 0, 1, 2
Y= 0 (X, Y) ( ,)
Y= 1 (X, Y) ( ,)
Y= 2 (X, Y) ( , )
*I’m having trouble understanding the route that should be taken to solve the equation. Am I suppose to plug each given y variable into the equation which will result in finding the x intercepts or is there a complete different method needed?
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
The wording of the problem, and the presentation of the data for the problem -- at least as you show it -- is confusing. My interpretation of the problem is this:
Given the function 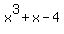 , find the coordinates of the points on the graph of the inverse function that have y coordinates of 0, 1, and 2.
Think of a point (a,b) on the graph of the function. The point (b,a) is on the graph of the inverse of the function.
So, when asked to find the coordinates of the point on the graph of the inverse function with y coordinate a, we evaluate the function at x=a to find the corresponding y value, giving us the coordinates (a,b) of a point on the graph of the function. Then we switch the x and y values to get the point (b,a) on the graph of the inverse function.
Once you understand what you are being asked to do (I THINK!!), it is easy.
Here is the first one: f(0) = -4, so (0,-4) is on the graph of the function; then the point (-4,0) is on the graph of the inverse. More specifically, it is THE point on the graph of the inverse function that has y coordinate 0.
You can do the other two....
|
|
|
