.
What are the solutions for sin(4x) + sin(x) = 0, in the interval [ ,
, ).
).
~~~~~~~~~~~~~~~~~~~~
Please pay attention on how I edited your condition.
sin(4x) + sin(x) = 0. (1)
Use the formula (one of the basic Trigonometry formula)
sin(a) + sin(b) = 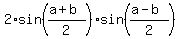 ,
which is valid for any angles "a" and "b".
By applying it, you get from (1)
,
which is valid for any angles "a" and "b".
By applying it, you get from (1)
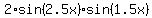 = 0.
Thus you must consider two separate cases.
a) sin(2.5x) = 0 ====> 2.5x = 0,
= 0.
Thus you must consider two separate cases.
a) sin(2.5x) = 0 ====> 2.5x = 0,  ,
,  ,
,  ,
,  ,
, 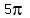 ====> x = 0,
====> x = 0, 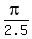 ,
, 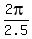 ,
, 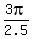 ,
, 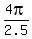 ,
, 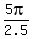 =
=  = same as 0,
and after that the roots repeat cyclically.
This row of solutions is the same as 0,
= same as 0,
and after that the roots repeat cyclically.
This row of solutions is the same as 0, 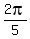 ,
, 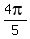 ,
, 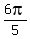 ,
, 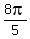 and
and 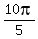 =
=  = same as 0.
In more compact form, this family of solutions is
= same as 0.
In more compact form, this family of solutions is 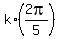 , k = 0, 1, 2, 3, 4.
b) sin(1.5x) = 0 ====> 1.5x = 0,
, k = 0, 1, 2, 3, 4.
b) sin(1.5x) = 0 ====> 1.5x = 0,  ,
,  ,
,  ====> x = 0,
====> x = 0, 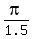 ,
, 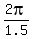 ,
, 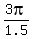 =
=  = same as 0,
and after that the roots repeat cyclically.
This row of solutions is the same as 0,
= same as 0,
and after that the roots repeat cyclically.
This row of solutions is the same as 0,  ,
,  ,
, 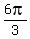 =
=  = 0.
In more compact form, this family of solutions is
= 0.
In more compact form, this family of solutions is 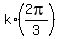 , k = 0, 2, 4.
Answer. There are two families of solutions:
a)
, k = 0, 2, 4.
Answer. There are two families of solutions:
a) 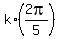 , k = 0, 1, 2, 3, 4 and b)
, k = 0, 1, 2, 3, 4 and b) 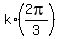 , k = 0, 2, 4.
, k = 0, 2, 4.
Solved.