|
Question 1127624: Find the distance from point A to XZ←→. Round your answer to the nearest tenth.
A(3,0) X(-1,-2) Z(2,7) Y(0,1)
Found 3 solutions by Alan3354, greenestamps, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the distance from point A to XZ. Round your answer to the nearest tenth.
A(3,0) X(-1,-2) Z(2,7) Y(0,1)
=========
Point Y is not involved.
---
There's more than 1 way to do this.
Method 1:
Find the slope of XZ.
Slope m = diffy/diffx
----
The distance from a point to a line is perpendicular to the line.
The slope of lines perpendicular is the negative inverse of the slope of the line, = -1/m
----
Use y-y1 = (-1/m)*(x-x1) where (x1,y1) is the point and -1/m is the slope of the perpendicular line.
======================
A 2nd method requires knowing a formula, which makes it less attractive IMO.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor Alan3354 said there was more than one way to work the problem; and then he outlined only one way. I'm not sure if that was his intention, or if he had intended to show a different method.
In any case, his solution method is a good one. Outlined, it says
(1) find the slope of XZ
(2) find the perpendicular slope
(3) find the equation of the line with the slope from (2) passing through A(3,0)
(4) find the point of intersection of XZ and the line from (3)
(5) find the distance from A to that intersection point
Note in fact the given point Y DOES become involved in the problem, because it turns out to be the point of intersection of the two lines.
Now here is another method that is very useful in problems like this. It's basically a formula that can be derived from the solution method described above.
SHORTEST DISTANCE FROM A GIVEN POINT TO A GIVEN LINE
If the equation is in the form Ax+By+C=0, the shortest distance from P(m,n) to the line is
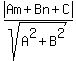
For this problem, the equation of XZ is y = 3x+1; in the form required for the formula, that is 3x-y+1=0. Then the shortest distance from (3,0) to that line is

Answer by ikleyn(52798)   (Show Source): (Show Source):
|
|
|
| |