|
Question 1127528: Determine algebraically whether the function f(x)=x^3-2x+1 is odd, even, or neither
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! To do this, you take the function and plug  in for in for  , and then , and then 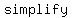 . .
If you end up with the exact same function that you started with (that is, if  , so all of the signs are the same), then the function is , so all of the signs are the same), then the function is  . .
If you end up with the exact opposite of what you started with (that is, if  , so all of the signs are switched), then the function is , so all of the signs are switched), then the function is  . .
In all other cases, the function is "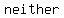 even nor odd". even nor odd".



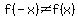 =>is not an =>is not an  function function
check if 

so, 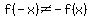 =>is not an =>is not an 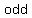 function function
so, answer is: 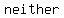
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The solution by mathlover1 is good, including descriptions of what makes a function even or odd.
For polynomial functions, the work is easier than what she shows.
The names "even function" and "odd function" come from the fact that any monomial function is even if the exponent is even and odd if the exponent is odd.
3 (the constant, exponent 0), x^2, x^4, and x^18 are even functions. That is easy to see, because replacing x with -x and raising to an even power gives the same result.
x, x^3, x^7, and x^73 are odd functions; again it is easy to see, because replacing x with -x and raising to an odd power gives the opposite result.
Then use the fact that a polynomial function is even or odd if and only if all the terms are either even or odd.
In the given function, the exponents on the variables are 3, 1, and 0. Since some are even and some are odd, the function is neither even nor odd.
|
|
|
| |