SOLUTION: If √x+√y=√45 and x and y are positive integers, then what is the value of √x+y?

Algebra ->  Equations -> SOLUTION: If √x+√y=√45 and x and y are positive integers, then what is the value of √x+y?      Log On


   

Question 1127469: If √x+√y=√45 and x and y are positive integers, then what is the value of √x+y?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

If sqrt%28x%29%2Bsqrt%28y%29=sqrt%2845%29+ and x+and y+are positive integers, then what is the value of sqrt%28x%29%2By?
sqrt%28x%29%2Bsqrt%28y%29=sqrt%2845%29+........solve for y
sqrt%28y%29=3sqrt%285%29+-sqrt%28x%29
%28sqrt%28y%29%29%5E2=%283sqrt%285%29+-sqrt%28x%29%29%5E2
y=%283%2Asqrt%285%29%29%5E2+-6%2Asqrt%285%29%2Asqrt%28x%29%2B%28sqrt%28x%29%29%5E2
y=9%2A5+-6%2Asqrt%285%29%2Asqrt%28x%29%2Bx
y+=+x+-+6%2A+sqrt%285%29%2A+sqrt%28x%29+%2B+45
then
sqrt%28x%29%2By=sqrt%28x%29%2Bx+-+6%2Asqrt%285%29%2Asqrt%28x%29+%2B+45
sqrt%28x%29%2By=sqrt%28x%29%281%2Bx+-+6%2Asqrt%285%29+%29+%2B+45

Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.

My reading of the problem is different from that of the tutor @MathLover1,

and my solution is different, too, as well as my answer. 

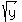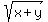    If  sqrt%28x%29 + sqrt%28y%29 = sqrt%2845%29  and x and y are positive integers, then what is the value of sqrt%28x%2By%29 ?


Solution 

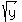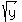sqrt%28x%29 + sqrt%28y%29 = sqrt%2845%29  ====>  


sqrt%28x%29 = sqrt%2845%29 - sqrt%28y%29  ====>  square both sides  ====>


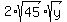x = 45 - 2%2Asqrt%2845%29%2Asqrt%28y%29 + y.   (*)


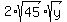Since x and y  in this equation are integers,  2%2Asqrt%2845%29%2Asqrt%28y%29 must be integer.


Hence, the factor "y" must complement the number 45 to a perfect square.


It implies that  y = 5.


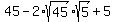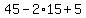Then from  (*)  x = 45+-+2%2Asqrt%2845%29%2Asqrt%285%29+%2B+5 = 45+-+2%2A15+%2B+5 = 20.


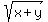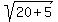Answer.  If  sqrt%28x%29+%2B+sqrt%28y%29 = sqrt%2845%29  and x and y are positive integers,  then  sqrt%28x%2By%29 = sqrt%2820%2B5%29 = sqrt%2825%29 = 5.

Solved.


Nice solution to a nice problem.


---------------

Specially for the tutor @MathLover1,  I'd like to explain,  why I think that my reading of the problem is correct. 

    We are given an info about the symmetric function  f(x,y) = sqrt%28x%29+%2B+sqrt%28y%29.


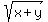    Therefore, the question should be (and, actually, MUST BE) about a symmetric function, too;  in this case, about the function  sqrt%28x%2By%29.