Question 1127410: find the centre,foci,vertices,and graph the following conics
1)8y²+12x=0
2)9x²-4y²-18x-16y-43=0
3)9x²+4y²-18x+16y-11=0
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the center,foci,vertices,and graph the following conics
1)
 -> Parabola with horizontal axis: -> Parabola with horizontal axis:
Vertex is ( , , ) )
Focus is ( , , ) )
Directrix is the line 
Axis is the line 


 ...i you compare to ...i you compare to  , you see that , you see that
=>  , ,  ->Vertex is ( ->Vertex is ( , , ) )
Axis is the line 
 -> ->  -> -> 
Focus is ( , , )->( )->(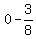 , , )->( )->( , , ) )
Directrix is the line  -> -> -> ->

2)
 ->hyperbola ->hyperbola





since  , , -> -> ; for ; for  part part  , ,  -> ->







Center is ( , , ) . ) .



 ->semi-major axis length ->semi-major axis length
 ->semi-minor axis length ->semi-minor axis length

center: ( , , ) )
vertices: ( , , ) and ( ) and ( , , ) )
foci: ( , ,  ) and ( ) and ( , ,  ) ≈( ) ≈( , ,  ) and ( ) and ( , ,  ) )

3)
 ->ellipse ->ellipse








 ->Ellipse with vertical major axis: ->Ellipse with vertical major axis:


 ->semi-major axis length ->semi-major axis length
 ->semi-minor axis length ->semi-minor axis length

center: ( , , ) )
foci : ( , ,  ) and ( ) and ( , ,  )≈( )≈( , ,  ) and ( ) and ( , ,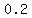 ) )
vertices: ( , ,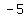 ) and ( ) and ( , ,  ) )

|
|
|