SOLUTION: Given that coordinates of P amd Q are (-2,6) and (9,3) , find a) cooridantes of point R that lies on y axis such that PR =QR b) coordinates of point S that lies on x axis such

Algebra ->  Inequalities -> SOLUTION: Given that coordinates of P amd Q are (-2,6) and (9,3) , find a) cooridantes of point R that lies on y axis such that PR =QR b) coordinates of point S that lies on x axis such       Log On


   

Question 1127181: Given that coordinates of P amd Q are (-2,6) and (9,3) , find
a) cooridantes of point R that lies on y axis such that PR =QR
b) coordinates of point S that lies on x axis such as PS=QS
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
given:
P amd Q are (-2,6) and (9,3) ,
find:

a) cooridantes of point R+that lies on y axis such that PR+=QR
if point R that lies on y+axis, cooridantes will be (0,y)
use distance formula to find y
(0,y) and (-2,6)
d=sqrt%28%28x-x%5B1%5D%29%5E2%2B%28y-y%5B1%5D%29%5E2%29
d=sqrt%28%280%2B2%29%5E2%2B%28y-6%29%5E2%29
d=sqrt%284%2B%28y-6%29%5E2%29


(0,y) and (9,3)
d=sqrt%28%28x-x1%29%5E2%2B%28y-y1%29%5E2%29
d=sqrt%28%280-9%29%5E2%2B%28y-3%29%5E2%29
d=sqrt%2881%2B%28y-3%29%5E2%29

=>
sqrt%284%2B%28y-6%29%5E2%29=sqrt%2881%2B%28y-3%29%5E2%29
4%2By%5E2-12y%2B36=81%2By%5E2-6y%2B9
-12y%2B40=-6y%2B90
-90%2B40=-6y%2B12y
6y=-50
y=-8.33
cooridantes of point 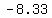R: (0,-8.33)

proof that PR+=QR
Solved by pluggable solver: Distance Between 2 points
The distance formula is sqrt%28%28%28x%5B2%5D-x%5B1%5D%29%5E2%29%2B%28%28y%5B2%5D-y%5B1%5D%29%5E2%29%29. Plug in the numbers,
sqrt%28%28%280-%28-2%29%29%5E2%29%2B%28%28-8.33-%286%29%29%5E2%29%29
sqrt%282%5E2%2B-14.33%5E2%29 The distance is 14.4688942217434.



PR+=14.47
Solved by pluggable solver: Distance Between 2 points
The distance formula is sqrt%28%28%28x%5B2%5D-x%5B1%5D%29%5E2%29%2B%28%28y%5B2%5D-y%5B1%5D%29%5E2%29%29. Plug in the numbers,
sqrt%28%28%280-%289%29%29%5E2%29%2B%28%28-8.33-%283%29%29%5E2%29%29
sqrt%28-9%5E2%2B-11.33%5E2%29 The distance is 14.4695853430567.



QR=14.47

b)
coordinates of point S that lies on x axis such as PS=QS
S that lies on x axis :(x,0)

distance formula again
(x,0) and (-2,6 )

d=sqrt%28%28x-x1%29%5E2%2B%28y-y1%29%5E2%29
d=sqrt%28%28x%2B2%29%5E2%2B%280-6%29%5E2%29
d=sqrt%28%28x%2B2%29%5E2%2B36%29

(x,0) and (9,3 )
d=sqrt%28%28x-x1%29%5E2%2B%28y-y1%29%5E2%29
d=sqrt%28%28x-9%29%5E2%2B%280-3%29%5E2%29
d=sqrt%28%28x-9%29%5E2%2B9%29
=>
sqrt%28%28x%2B2%29%5E2%2B36%29=sqrt%28%28x-9%29%5E2%2B9%29
%28x%2B2%29%5E2%2B36=%28x-9%29%5E2%2B9
x%5E2%2B4x%2B4%2B36=x%5E2-18x%2B81%2B9

4x%2B40=-18x%2B90
4x%2B18x=90-40
22x=50
x=2.272727272727273
x=2.27

so, the point S is at (2.27,0)
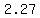proof: PS=QS
Solved by pluggable solver: Distance Between 2 points
The distance formula is sqrt%28%28%28x%5B2%5D-x%5B1%5D%29%5E2%29%2B%28%28y%5B2%5D-y%5B1%5D%29%5E2%29%29. Plug in the numbers,
sqrt%28%28%282.27-%28-2%29%29%5E2%29%2B%28%280-%286%29%29%5E2%29%29
sqrt%284.27%5E2%2B-6%5E2%29 The distance is 7.36429901619971.



PS=7.36
Solved by pluggable solver: Distance Between 2 points
The distance formula is sqrt%28%28%28x%5B2%5D-x%5B1%5D%29%5E2%29%2B%28%28y%5B2%5D-y%5B1%5D%29%5E2%29%29. Plug in the numbers,
sqrt%28%28%282.27-%289%29%29%5E2%29%2B%28%280-%283%29%29%5E2%29%29
sqrt%28-6.73%5E2%2B-3%5E2%29 The distance is 7.3683715975784.



QS=7.36