Question 1127127: For a gift exchange 10 people names are written on slips of paper and placed in a bowl. The slips of paper are mixed up and, each person selected one name.
a) what is the probability that everyone select their own name?
b) what is the probability that nobody selects his or her own name?
The answer for a) is about 2.7557(10^7)
The answer for b) 1-2.7557(10^-7) I donít know they got that please help thank u
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To solve the problem (and to understand the solution), you need to be familiar with permutations.
Are you familiar with it ?
If not, look into the lessons
- Introduction to Permutations
- PROOF of the formula on the number of Permutations
- Problems on Permutations
in this site.
For example, to answer a), you need to know that there are 10! = 10*9*8*7*6*5*4*3*2*1 permutations of 10 objects,
and only one of them is the identical permutation.
In other words, there are 10! = 10*9*8*7*6*5*4*3*2*1 possible outcomes in this game, and only one of them is favorable.
It gives the answer for a): Probability = 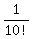 = = 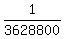 = = 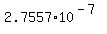 . .
Notice that your answer for a) is written INCORRECTLY.
The answer for b), which you printed in your post, is incorrect, too.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To add to the response by tutor @ikleyn....
The answer to part b can't be 1 - 2.7557*10^-7. That would make the sum of the answers to parts a and b equal to 1.
That would imply that the only possible outcomes are each person getting his own name or no people getting their own names. That leaves out the large number of outcomes where some but not all of the people get their own names.
|
|
|