SOLUTION: One landscaper can till the soil for a lawn in 30 min, whereas a second landscaper needs only 15 min to do the same job. How long will it take to till the soil for the lawn with bo

Algebra ->  Rate-of-work-word-problems -> SOLUTION: One landscaper can till the soil for a lawn in 30 min, whereas a second landscaper needs only 15 min to do the same job. How long will it take to till the soil for the lawn with bo      Log On


   

Question 1127109: One landscaper can till the soil for a lawn in 30 min, whereas a second landscaper needs only 15 min to do the same job. How long will it take to till the soil for the lawn with both landscapers working together?
Rate of work Time Worked Portion of work
Finished
1St
person 1/30 x w = w/30
2nd
person 1/15 x w = w/15
Would you add w/30 + w/15 = w/10?
Please help me find how long it would take both workers to complete the job together.
Found 3 solutions by josgarithmetic, MathTherapy, greenestamps:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
One Landscaper, %281%2F30%29%28lawn%2Fminutes%29

Second Landscaper, %281%2F15%29%28lawn%2Fminutes%29

Both Together, 1%2F30%2B1%2F15=1%2F30%2B2%2F30=3%2F30=1%2F10

The combined rate means ONE lawn tilled in TEN minutes.

10%28minutes%2Flawn%29

Answer by MathTherapy(10556) About Me  (Show Source):
You can put this solution on YOUR website!

One landscaper can till the soil for a lawn in 30 min, whereas a second landscaper needs only 15 min to do the same job. How long will it take to till the soil for the lawn with both landscapers working together?
Rate of work Time Worked Portion of work
Finished
1St
person 1/30 x w = w/30
2nd
person 1/15 x w = w/15
Would you add w/30 + w/15 = w/10?
Please help me find how long it would take both workers to complete the job together.
IGNORE the other person who's in a different world. 

In answer to your question, and since it appears that you used w as the time  worked, you do add 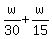w%2F30+%2B+w%2F15, but the equation to solve to get w,

or the time both worked is: highlight_green%28matrix%281%2C3%2C+w%2F30+%2B+w%2F15%2C+%22=%22%2C+1%29%29, since the Time worked by the slower person, times the slower person's rate, PLUS (+) the Time worked 

by the faster person, times the faster person's rate, equals 1, with 1 being the entire job or 100% of the work.

Solve that for w, and you'll get the time spent by both to do the job, together.

Answer by greenestamps(13209) About Me  (Show Source):
You can put this solution on YOUR website!


The presentation of the solution by @josgarithmetic, as I see it, is valid; but it's hard (for me, at least) to follow and understand.

If indeed you are using w for the amount of time worked, then the path to the solution can be by solving the equation as shown by @maththerapy in his response.

But I think you can solve the problem with less work by a slightly different method.

Instead of using a variable w to represent the amount of time worked, think purely in terms of the fraction done by each worker in 1 minute.

One worker can do the job in 30 minutes, so he does 1/30 of the job in 1 minute; the other worker similarly does 1/15 of the job in 1 minute.

So together the fraction of the job they do in 1 minute is 1/30+1/15 = 1/10.

Then, since together they do 1/10 of the job in 1 minute, it takes then 10 minutes to do the job together.

All three solution methods are valid; look at each of them and use the one that makes the most sense to you.