SOLUTION: Find the remainder when 2 raised to 512 is divided by 14

Let  

    r = 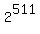 mod 7     (1)

be the remainder of division the integer number 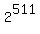  by 7.


Then the remainder   mod 14  is (2r).


Therefore, to answer the problem question, it is ENOUGH to find  r = 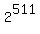 mod 7   and then double it.


The remainders of division    by 7 form a cyclical sequence

    2, 4, 1,  2, 4, 1, . . .   for  n = 1, 2, 3, 4, 5, 6,  . . .    (2)

with the length of the cycle equal 3.


r = 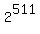 mod 7   is 511-th term in this periodical/cycling sequence.  


Since  511 = 510+1 = 170*3 + 1,   511-th term in this periodical/cycling sequence is the first term of the basic cycle.


Hence,  r = 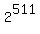 mod 7  is equal to 2.


Therefore, the value of (2r), which is the problem question, is 4.