SOLUTION: Hi! I have a college algebra problem and I don't know how to set it up. The problem says: A shopper spends half her money in the first shop she visits. In the second shop she

Click here to see ALL problems on Money Word Problems

Question 1127044: Hi!
I have a college algebra problem and I don't know how to set it up. The problem says:
A shopper spends half her money in the first shop she visits. In the second shop she spends 1/3 of what remains. In the third shop she spends $25. She then has $15 left. How much had she at the start?
Thank you!
-Maddie
Found 3 solutions by josgarithmetic, MathLover1, greenestamps:
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website!
----
spends half her money in the first shop she visits. In the second shop she spends 1/3 of what remains. In the third shop she spends $25. She then has $15 left. How much had she at the start?
----

x, starting amount

After first shop
remains

After second shop

remains

After third shop

-

check:
shop 1
60 remain.
shop 2
40 remain.
shop 3
40-25=15

Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!

let�s say she has
if she spends half her money in the first shop she visits, we have
she spend
=>remains
in the second shop she spends of what remains:

in the third shop she spends $
she then has $ left
she at the start money and it should be equal to sum of all money she spent plus $ she has left
......solve for , both sides multiply by

check:
in the first shop she spend
in the second shop she spends (or )
in the third shop she spends $
she then has $
add all together:

Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

There are many ways to solve a problem like this. I have no idea what kind of solution is expected in a college algebra course.

Here is one way to solve the problem using formal algebra -- that is, writing and solving an equation.

Let the amount she started with be x.

At the first shop, what she spends is 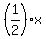; the amount she has left is .

At the second shop, she spends (1/3) of what she has left -- that is, . The amount she has left is .

After that, she spends $25 and has $15 left; that means she had $40 left after the second shop.

So the $40 she has left after the second shop is (1/3)x:

She started with $120.

CHECK:
$120 - (1/2)($120) = $120-$60 = $60
$60 - (1/3)($60 = $60-$20 = $40
$40-$25 = $15

That is a really ugly way to solve the problem. In my opinion, the easiest way to solve the problem is to think in terms of the fractions she has left, rather than the fractions she spends. Like this:

She starts with x and spends half at the first shop; what she has left is 1/2 of what she started with.

So she goes to the second shop with half of what she started with. When she SPENDS 1/3 of what she has left in the second shop, what she HAS LEFT is 2/3 of what she had when she got to the second shop. 2/3 of half of x is 1/3 of x.

So after the second shop, she has 1/3 of what she started with. And what she has left at that point is the $25 she spent in the third shop, plus the $15 she had left after the third shop, for a total of $40.

So 1/3 of what she started with is $40; that means what she started with was $120.

Expressing all that in shorter form, the amount she started with gets multiplied by 1/2 in the first shop and then by 2/3 in the second shop, leaving her with $40.

In algebraic notation, that solution looks like this:

And there are many other ways of solving the problem. Perhaps you will get another response from another tutor showing a method you like better....