SOLUTION: As a planet orbits around the Sun, it traces out an ellipse. If the center of the ellipse were placed at (0,0) on a coordinate grid, the sun would actually be off-centered (located

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: As a planet orbits around the Sun, it traces out an ellipse. If the center of the ellipse were placed at (0,0) on a coordinate grid, the sun would actually be off-centered (located      Log On


   

Question 1126874: As a planet orbits around the Sun, it traces out an ellipse. If the center of the ellipse were placed at (0,0) on a coordinate grid, the sun would actually be off-centered (located at the focus of the ellipse).
The aphelion (maximum distance from the Sun) of the planet Mars is approximately 156 miles, while the perihelion (minimum distance from the Sun) of Mars is about 128 million miles. Use this information to find the lengths of the semi major and semi minor axes, rounded to the nearest million. If Mars has an orbital velocity of 54,000 miples per hour (1.296 miles per day), how many days does it take Mars to orbit the Sun?
Answer by ikleyn(52785) About Me  (Show Source):
You can put this solution on YOUR website!
.
As a planet orbits around the Sun, it traces out an ellipse. If the center of the ellipse were placed at (0,0) on a coordinate grid,
the sun would actually be off-centered (located at the focus of the ellipse).

The aphelion (maximum distance from the Sun) of the planet Mars is approximately 156 miles,
while the perihelion (minimum distance from the Sun) of Mars is about 128 million miles.
Use this information to find the lengths of the semi major and semi minor axes, rounded to the nearest million.
If Mars has an orbital velocity of 54,000 miples per hour (1.296 miles per day), how many days does it take Mars to orbit the Sun?
~~~~~~~~~~~~~~~~~~~ 


Let "a" be the semi-major axis length (in millions miles); and

let "c" be the focal distance.


Then the condition says that


a + c = 156   (million miles)   (1)
a - c = 128   (million miles)   (2)


From (1) and (2) it follows (by adding the equations)


2a = 156 + 128 = 284  ====>  a = 284/2 = 142  million miles  (semi-major axis).


Then from (1)  c = 156 - 142 = 14  million miles  (linear eccentricity).


Then semi-minor axis  b = 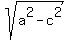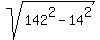sqrt%28a%5E2+-+c%5E2%29 = sqrt%28142%5E2-14%5E2%29 = 141.3 million miles.

------------------

In this post, the dimension units and the numbers were given VERY INACCURATELY.

I have no any intention (and actually have no any time) to edit the author of this post, so I will stop at this point. 


Dear author !


    If you ask for help (at the free of charge basis), if you want the tutors work for you spending their valuable time, 

    then  you MUST do EVERYTHING from your side  to make your post clear, precise and correct.


Excuse for teaching you these truisms !