Question 1126668: Solve the following:
2/A - 3/B = -1 [1]
5/A - 6/B = -1/2 [2]
Multiply [1] by 2:
4/A + 6/B = -2
Not sure how to solve. Non-homework.
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The standard method for solving such problems is introducing new variables
x =  , y = , y = 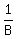 .
Then your system takes the form
2x - 3y = -1 (1)
5x - 6y = -1/2 (2)
To solve it, multiply eq(1) by 2 (both sides) and then subtract from eq(2). You will get
5x - 2*(2x) = .
Then your system takes the form
2x - 3y = -1 (1)
5x - 6y = -1/2 (2)
To solve it, multiply eq(1) by 2 (both sides) and then subtract from eq(2). You will get
5x - 2*(2x) =  - 2*(-1), or
9x - 4x = - 2*(-1), or
9x - 4x =  + 2,
x = 1.5.
Then from eq(1), 2*1.5 -3y = -1, 3 - 3y = -1, 3 + 1 = 3y ====> y = + 2,
x = 1.5.
Then from eq(1), 2*1.5 -3y = -1, 3 - 3y = -1, 3 + 1 = 3y ====> y =  .
Now you have x = 1.5 = .
Now you have x = 1.5 =  ====> A = ====> A =  = = 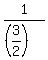 = =  and
y = and
y =  = = 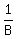 ====> B = ====> B =  .
Answer. A = .
Answer. A =  and B = and B =  . .
Solved.
Simply and elegantly.
-------------
The way which @josgarithmetic tries to sell you - is the way to NOWHERE.
For your safety, simply ignore it.
===============
For your safety, ignore EACH and EVERY HIS POST . . . . . . . .
I just tired to fix all this RUBBISH after him.
/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
Regarding the post by @greenestamps, he writes
You certainly CAN introduce new variables to solve the problem, as tutor @ikleyn does. But you can solve the problem without doing that.
Truly, you can try solve the problem without doing that.
But then I guarantee you that you as inexperienced person in solving such problems, will make about 20 errors
on the way and will not be able to complete the solution correctly.
The way I showed you in my post - is simplest, straightforward and prevents you of making crude errors.
It is not without reasons the way I presented you in my post is considered as the standard and canonical.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) 2/A - 3/B = -1
(2) 5/A - 6/B = -1/2
You certainly CAN introduce new variables to solve the problem, as tutor @ikleyn does. But you can solve the problem without doing that.
In the work you show, multiplying the first equation by 2 gives
4/A - 6/B = -2
You incorrectly show that equation as
4/A + 6/B = -2.
Let's continue with the way you were going....
The two equations are now
(1) 4/A - 6/B = -2
(2) 5/A - 6/B = -1/2
To eliminate variable B, you need to subtract one equation from the other. If you do that correctly, you will end up with
1/A = 3/2
Substituting this value for 1/A in the original first equation finds the value of 1/B:
2/A - 3/B = -1 <-- (these 2 lines added in revised answer, after reader in quiry)
2(3/2)-3/B = -1 <-- (these 2 lines added in revised answer, after reader in quiry)
3 - 3/B = -1
4 = 3/B
4/3 = 1/B
We now have 1/A = 2/3 and 1/B = 4/3, so the solutions are
A = 3/2; B = 3/4
Just a note about solving this problem by eliminating one variable....
When you multiplied the first equation by 2, you then had to subtract one equation from the other to eliminate B. Subtracting equations is more likely to produce errors than adding equations. So multiply the first equation by -2 instead of 2; that will allow you to eliminate B by ADDING the two equations:
-4/A + 6/B = 2
5/A - 6/B = -1/2
1/A = 3/2
---------------------------------------
response revised, 2 lines added, see above
|
|
|