Question 1126540: A play sells lower level tickets for $87 and upper level tickets for $62. On the opening night 2723 tickets were sold for a total $215801.
Please explain where the numbers you get throughout the equation come from. I have tried following examples but half way through the example a random number gets thrown into the equation and I don't know where it comes from. If I understood this I could maybe finally do this with ease.
Answer by sbro7568(4)   (Show Source):
You can put this solution on YOUR website! To represent the number of lower level tickets sold, we will use the variable L, and to represent the number of upper level tickets sold, we will use the variable U.
Since the lower level tickets cost $87 and the upper level tickets cost $62, the equation of the total money earned must be 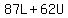 . When we plug in the total earnings provided, we get  .
The total number of tickets sold was 2723, therefore we can put together another equation, as follows:  .
Now, if we multiply the second equation by -87 on both sides, we get  . If we then add the two equations together, the 87L and the -87 L cancel out, resulting in  . We can then divide both sides by -25 to solve for U, ending up with U = 844. Then, we can plug U into the second equation above and solve for L, and get  .
I assume the number you are confused about in the equations is the -87 that we multiplied the second equation by. This number simply needed to be there so that we could cancel out one variable and be able to solve for the other. It also could have been -62, cancelling out 62U in the original equation and having us solve for L first. To get this number for other similar problems, simply take the constant for one of the variables in the original equation and change it to a negative.
--
tl;dr:
|
|
|
