Question 1126419: A movie theater charges $9 for an adult’s ticket, $7 for a senior ticket and $6 for a child’s ticket. For a particular movie, the theater sold a total of 290 tickets, which brought in $2400. The number of seniors’ tickets sold was twice the number of children’s tickets sold. Determine the number of adults’, seniors’, and children’s tickets sold.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620)   (Show Source):
Answer by ikleyn(52798)  (Show Source):
You can put this solution on YOUR website! .
Let "x" be the number of the children tickets.
Then the number of the senior tickets is 2x, according to the condition,
and the number of adult tickets is (290 - x - 2x) = (290-3x).
Then the money equation is
6x + 9*(290-3x) + 7*(2x) = 2400 dollars.
Simplify and solve for x:
6x + 9*290 - 27x + 14x = 2400
-7x = 2400 - 9*290
x = 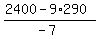 = 30.
Answer. 30 children tickets; 2*30 = 60 senior tickets and 290 - 30 - 60 = 200 adult tickets.
Check. 6*30 + 9*200 + 7*60 = 24000 dollars. ! Correct !
Solved.
------------------
In this way, you can easily solve the problem using one equation and one unknown.
I think (129% sure) that this problem was designed and was intended to be solved exactly in this way.
===============
See the lessons
- Advanced word problems to solve using a single linear equation
- HOW TO algebreze and solve these problems using one equation in one unknown
in this site, where you will find many other similarly solved problems.
|
|
|
