SOLUTION: A circular piece of metal is to be cut into 3 pieces of one size and 5 pieces of a larger size so that the degree measure of the central angle of the larger piece is 6 degrees less

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: A circular piece of metal is to be cut into 3 pieces of one size and 5 pieces of a larger size so that the degree measure of the central angle of the larger piece is 6 degrees less      Log On


   

Question 1126403: A circular piece of metal is to be cut into 3 pieces of one size and 5 pieces of a larger size so that the degree measure of the central angle of the larger piece is 6 degrees less than twice the degree measure of each smaller piece. What is the degree measure of each of the larger pieces?
Answer by ikleyn(52855) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let x be the degree measure of each smaller piece.


Then the degree measure of each larger piece is (2x-6).


Your equation is 


    3x + 5*(2x-6) = 360  degrees.


Solve for x:


    3x + 10x - 30 = 360

    13x = 360 + 30 = 390

    x = 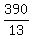390%2F13 = 30 degrees.


Answer.  The smaller piece has the central angle of 30 degrees;

         The larger piece has the central angle of 2*30 - 6 = 54 degrees.

Solved.