Question 1126050: A tortoise and a hare are competing in a 1600-meter race. The arrogant hate decides to let thebtortoise have a 580-meter head start. When the start gun is fired the hare begins running at a constant speed of 8 meters per second and the tortoise begins crawling at a constant speed of 5 meters per second.
Let t represent the number of seconds that have elapsed since the start gun was fired.
A) write an expression in terms of t that represents the hares distance from the starting line (in meters).
B) write an expression in terms of t that represents the tortoises distance from the starting line (in meters).
C) write an expression in terms of t that represents the number of meters the tortoise is ahead of the hare.
D) who finished the race first ?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! rate * time = distance (R * T = D)
the hare runs at 8 meters a second.
the tortoise crawls at 5 meters a second.
for the hare, the formula becomes 8 * T = D.
for the tortoise, the formula becomes 5 * T = D.
answers to your questions below:
A) write an expression in terms of T that represents the hare's distance from the starting line (in meters).
for the hare, rate * time = distance becomes 8 * T = D.
flip sides to get D = 8 * T.
this equation already tells you the hare's distance from the starting line in terms of T.
the expression you are looking for is 8 * T.
B) write an expression in terms of t that represents the tortoises distance from the starting line (in meters).
for the tortoise, rate * time = distance becomes 5 * T = D.
flip sides to get D = 5 * T.
this equation already tells you the tortoise's distance form the starting line in terms of T.
the expression you are looking for is 5 * T.
C) write an expression in terms of t that represents the number of meters the tortoise is ahead of the hare.
the tortoise gets a 580 meter head start.
for the hare, the equation is still D = 8 * T.
for the tortoise, the equation becomes D = 5 * T + 580.
what does this mean?
when T = 0, the hare has run a total of 0 meters and the hare has run a total of 580 meters (his head start).
as time goes on, the hare will get closer and closer to the tortoise and will eventually overtake him because the hare is traveling at a faster rate than the tortoise.
to find how many seconds the hare takes to catch up to the tortoise, set the distance for each equal.
since D for the hare is 8 * T and D for the tortoise is 5 * T + 580, set 8 * T = 5 * T + 580 and solve for T.
solve as follows:
subtract 5T from both sides of this equation to get 3T = 580.
divide both sides of this equation by 3 to get T = 580 / 3 = 193.333 rounded to 3 decimal places.
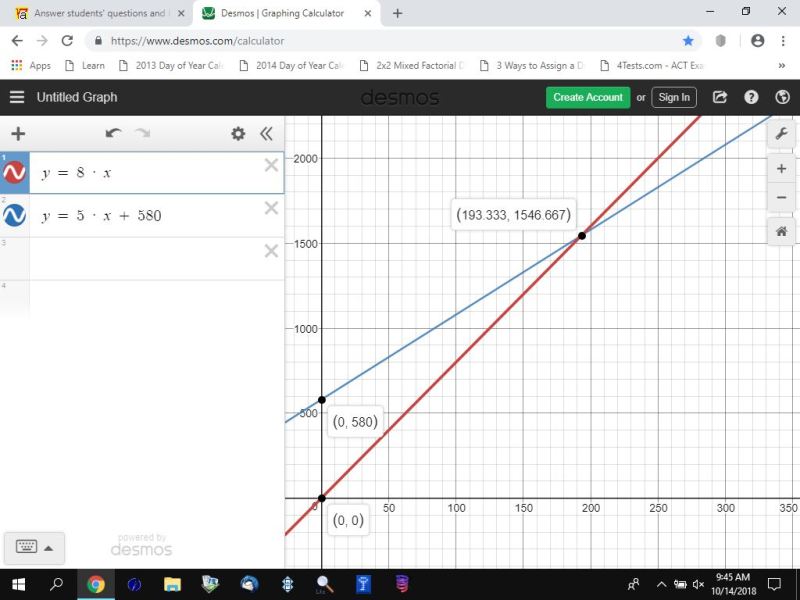
the hare will catch up to the tortoise in 193.333 seconds.
this can be seen on the first graph.
to find out who wins the race algebraically, set D = 1600 and solve for T in both equations.
D = 8 * T becomes 1600 = 8 * T.
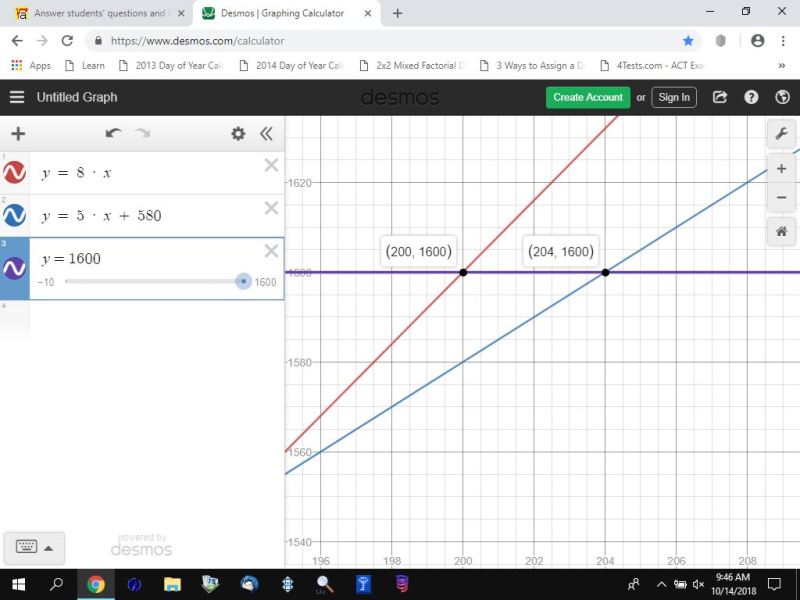
divide both sides of this equation by 8 to get T = 1600 / 8 = 200 seconds.
D = 5 * T + 580 becomes 1600 = 5 * T + 580
subtract 580 from both sides of the equation to get 1600 - 580 = 5 * T.
simplify to get 1020 = 5 * T
divide both sides of this equation by 5 and solve for T to get T = 1020 / 5 = 204 seconds.
this can be shown on the second graph.
the first graph shows that the hare catches up to the tortoise in 193.333 seconds.
the second graph shows that the hare completes the 1600 meter run in 200 seconds while the tortoise completes is in 204 seconds.
here's the graphs.
D) who finished the race first ?
the hare.
in the graphs, the equation for the hare is in red and the equation for the tortoise is in blue.
the horizontal line is in purple and is used to allow me to show you the number of seconds it takes for the hare and the tortoise to reach the 1600 meter mark.
the coordinate points are in (x,y) format.
x is the number of seconds.
y is the number of meters achieve in x seconds.
|
|
|