SOLUTION: How much money should be deposited into an account that earns 4.6% interest,compounded every month,so that after 20 years there is a balance of $24,000?

Algebra ->  Customizable Word Problem Solvers  -> Finance -> SOLUTION: How much money should be deposited into an account that earns 4.6% interest,compounded every month,so that after 20 years there is a balance of $24,000?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1125957: How much money should be deposited into an account that earns 4.6% interest,compounded every month,so that after 20 years there is a balance of $24,000?
Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.

It is a classic Ordinary Annuity saving plan. The general formula is 


    FV = P%2A%28%28%281%2Br%29%5En-1%29%2Fr%29,    


where  FV is the future value of the account;  P is the monthly payment (deposit); r is the monthly percentage yield presented as a decimal; 
n is the number of deposits (= the number of years multiplied by 12, in this case).


From this formula, you get for for the monthly payment 


    P = FV%2A%28r%2F%28%281%2Br%29%5En-1%29%29.     (1)


Under the given conditions, FV = $24,000;  r = 0.046/12;  n = 20*12.  So, according to the formula (1), you get for the monthly payment 


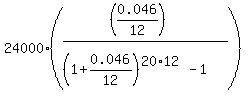    P = 24000%2A%28%28%280.046%2F12%29%29%2F%28%281%2B0.046%2F12%29%5E%2820%2A12%29-1%29%29%29 = $61.14.


Answer.  The necessary monthly deposit value is $61.14.


Note that of projected $24,000 the total of deposits will be only  20*12 times $61.14, i.e. 20*12*61.14 = 14673.60 dollars.
The rest is what the account will earn/accumulate in 20 years.

---------

On Ordinary Annuity saving plans,  see the lessons
    - Ordinary Annuity saving plans and geometric progressions
    - Solved problems on Ordinary Annuity saving plans
in this site.