Question 1125911: Use the matrix method to write the particular equation of a function in the form y=ax^2+bx+c
Containing (0,5) (2,13) and (3,26)
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Unfortunately, the other tutor wrote her first equation incorrectly (using the point (5,0) instead of (0,5); so all her work was wasted....
Given any system of equations, there are endless different paths to get to the solution using the matrix method (by which I assume you mean Gauss-Jordan elimination). Here is the path I followed.
Initial matrix:

The first thing I'm going to do is switch rows 1 and 3, because the current row 1 is in exactly the form I want for row 3:

First objective: make (1,1) entry equal to 1. I choose to avoid fractions where possible, so, instead of dividing row 1 by 9, I'm going to replace row 1 with row 1 minus 2 times row 2 (9-4*2 = 1):
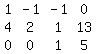
Next objective: get (2,1) and (3,1) entries equal to 0. (3,1) entry is already 0; to get (2,1) entry equal to 0, replace row2 with row 2 minus 4 times row 1:

Next objective: get (2,2) entry equal to 1. The only choice is to divide row 2 by 6:

Next objective: get (1,2) entry equal to 0 using the 1 in (2,2):

Next objective: get (1,3) and (2,3) equal to 0 using the 1 in (3,3):

The solution to the system is a=3, b=-2, c=5; the polynomial is

|
|
|