SOLUTION: Write the equation of the perpendicular bisector of the line segment with endpoints (-4,1) and (4,-3)

Algebra ->  Length-and-distance -> SOLUTION: Write the equation of the perpendicular bisector of the line segment with endpoints (-4,1) and (4,-3)      Log On


   

Question 1125712: Write the equation of the perpendicular bisector of the line segment with endpoints (-4,1) and (4,-3)
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
Write the equation of the perpendicular bisector of the line segment with endpoints
(-4,1) and (4,-3)
first find the equation of the line containing the segment with endpoints at (-4,1) and (4,-3) :
y=mx%2Bb
use given points to find a slope:
m=%28y%5B1%5D-y%5B2%5D%29%2F%28x%5B1%5D-x%5B2%5D%29
m=%281-%28-3%29%29%2F%28-4-4%29
m=%281%2B3%29%2F%28-4-4%29
m=+4%2F%28-8%29
m=+-1%2F2
y=-%281%2F2%29x%2Bb
use one point to find b
y=-%281%2F2%29x%2Bb...........(-4,1)
1=-%281%2F2%29%28-4%29%2Bb
1=+2%2Bb
1-2=b
b=-1
equation is: y=-%281%2F2%29x-1
now, recall:
A bisector cuts a line segment into two congruent parts. A segment bisector is called a perpendicular bisector when the bisector intersects the segment at a right angle.
the perpendicular bisector passes through the midpoint
so, first find the coordinates of the midpoint:
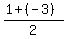(%28-4%2B4%29%2F2,%281%2B%28-3%29%29%2F2)
(0,-1)
since bisector perpendicular to line segment, it is also perpendicular to line y=-%281%2F2%29x-1
and perpendicular lines have slopes negative reciprocal to each other
so, the perpendicular bisector will have a slope m%5Bp%5D=-1%2Fm
m%5Bp%5D=%28-1%29%2F%28-1%2F2%29

m%5Bp%5D=+2
y=+2x%2Bb....use midpoint (0,-1) to find b
-1=+2%2A0%2Bb
b=-1
highlight%28y=+2x-1%29->the equation of the perpendicular bisector