Question 1125632: Juan drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 8 hours. When Juan drove home, there was no traffic and the trip only took 6 hours. If his average rate was 16 miles per hour faster on the trip home, how far away does Juan live from the mountains?
Found 4 solutions by josgarithmetic, MathTherapy, ikleyn, greenestamps:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by MathTherapy(10553)   (Show Source): (Show Source):
You can put this solution on YOUR website! Juan drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 8 hours. When Juan drove home, there was no traffic and the trip only took 6 hours. If his average rate was 16 miles per hour faster on the trip home, how far away does Juan live from the mountains?
The equation you need is:  : Thanks, tutor @Ikleyn! : Thanks, tutor @Ikleyn!
Solve this for D, the distance between home and the mountains!
Answer by ikleyn(52805)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Juan drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 8 hours.
When Juan drove home, there was no traffic and the trip only took 6 hours. If his average rate was 16 miles per hour
faster on the trip home, how far away does Juan live from the mountains?
~~~~~~~~~~~~~~~~~
The correct "speed" equation is
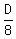 + 16 = + 16 =  ,
where D is one way distance.
The equation says that the speed at the 6-hours trip (the right side) was 16 miles per hour faster than at the 8-hours trip.
To solve the equation, multiply both sides by 24. You will get
3D + 16*24 = 4D, or
D = 16*24 = 384 miles.
Answer. One way distance is 384 miles. ,
where D is one way distance.
The equation says that the speed at the 6-hours trip (the right side) was 16 miles per hour faster than at the 8-hours trip.
To solve the equation, multiply both sides by 24. You will get
3D + 16*24 = 4D, or
D = 16*24 = 384 miles.
Answer. One way distance is 384 miles.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You already have three responses showing you versions of the usual algebraic method for solving the problem. Let me suggest an alternative which, for me at least, is faster and easier.
The distances are the same, and the ratio of the two times is 4:3. That means the ratio of the speeds is 3:4.
Using any one of a large number of methods, use that ratio and the fact that the higher speed is 16mph faster than the lower, and you get the speeds for the two parts of the trip as 48 and 64mph.
So then the distance is 48*8 = 384 miles, or 64*6 = 384 miles.
|
|
|