Question 1125238: Given: E(-2,3) F(-2,-2) G(3,-2) H(3,3)
Prove: EFGH is a rhombus
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ways to prove that a quadrilateral is a rhombus:
Show that it has four congruent sides. ( by definition of rhombus)
Given:
E( , , ) )
F( , , ) )
G( , , ) )
H( , , ) )
Prove: EFGH is a rhombus
find distance between two points: , , 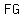 , , , and , and 
E( , , ) )
F( , , ) )





F( , , ) )
G( , , ) )






G( , , ) )
H( , , ) )





E( , , ) )
H( , , ) )





as you can see, all sides are same length which proves that a quadrilateral is a 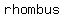
|
|
|