.
a) 0 envelopes in the box #3: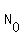 
= 
+ 
+ 
+ 
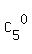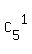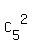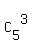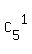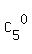+ + = 1 + 5 + 10 + 10 + 5 + 1 = 32 ways.
b) 1 envelope in the box #3: 
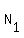= 5*(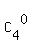
+ 
+ 
+ 
+ 
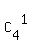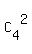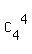) = 5*(1 + 4 + 6 + 4 + 1) = 80 ways.
c) 2 envelopes in the box #3: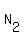 
= 10*(
+ 
+ 
+ 
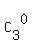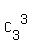) = 10*(1 + 3 + 3 + 1) = 80.
d) 3 envelopes in the box #3: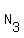 
= 10*(
+ 
+ 
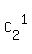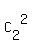) = 10*(1 + 2 + 1) = 40 ways.
e) 4 envelopes in the box #3: 
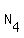= 5*(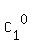
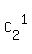+ ) = 5*2 = 10 ways.
f) 5 envelopes in the box #3: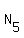 
= 1 way.
The total is the sum 32 + 80 + 80 + 40 + 10 + 1 = 243 ways.
Answer. 243 ways.
-----------------
The formulas in this post are SELF-EXPLANATORY.
If you have questions or if you need explanations, look into the formulas until they tell you the whole story.
==================
Notice that 243 = 
, and it is not eventually.
There is another way to calculate it, which gives the same result, but is much shorter and much more elegant.
You need to consider the binomial expansion of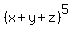 
as the sum
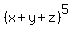= sum of all 
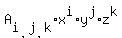with the coefficients 
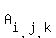, i + j + k = 5.
Each particular term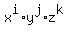 
with i + j + k = 5 "marks" each possible particular distribution
of envelopes in three boxes called "x", "y" and "z".
The number of all possible distributions is the sum of all coefficients 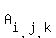, and it is equal to
the value of 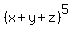at x= 1, y= 1, z= 1, which is exactly 
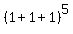= = 243.
This problem is for an advanced Math circle / Math Olympiad level.
Therefore, I will not go further into details - the idea is just presented very clearly for an adequate person.
