Consider the following linear program:
Min 2A + 2B
s.t.
1A + 3B ≤ 12
3A + 1B ≥ 13
1A - 1B ≥ 3
A, B ≥0
Change the problem to x's and y's by arbitrarily choosing
x = A and y = B
Consider the following linear program:
Min 2x + 2y
s.t.
1x + 3y ≤ 12
3x + 1y ≥ 13
1x - 1y ≥ 3
x, y ≥ 0
a. Show the feasible region.
b. What are the extreme points of the feasible region?
c. Find the optimal solution using the graphical solution procedure.
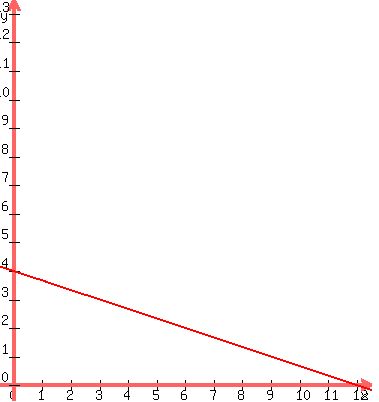
The boundary line for 1x + 3y ≤ 12 has the equation which is
like the inequality but has an equal sign in place of the
inequality symbol. So the boundary line for 1x + 3y ≤ 12 has the
equation 1x + 3y = 12. It has y-intercept (0,4) and x-intercept
(12,0) and is the red line. Since the origin (0,0) substituted for
(x,y) in the inequality 1x + 3y ≤ 12 gives 0 ≤ 12, the
solution set for the inequality 1x + 3y ≤ 12 is ON THE SAME
SIDE of the line as the origin is on, and since the origin is BELOW and
LEFT of the RED line, the solution set is BELOW and LEFT of its boundary line, the RED LINE.
 ---
The boundary line for 3x + 1y ≥ 13 has the equation which is
like the inequality but has an equal sign in place of the
inequality symbol. So the boundary line for 3x + 1y ≥ 13 has the
equation 3x + 1y = 13. It has y-intercept (0,13) and x-intercept
(
---
The boundary line for 3x + 1y ≥ 13 has the equation which is
like the inequality but has an equal sign in place of the
inequality symbol. So the boundary line for 3x + 1y ≥ 13 has the
equation 3x + 1y = 13. It has y-intercept (0,13) and x-intercept
(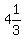 ,0) and is the GREEN line. Since the origin (0,0) substituted for
(x,y) in the inequality 3x + 1y ≥ 13 gives 0 ≤ 13, which is
FALSE, the solution set for the inequality 1x + 3y ≥ 12 is ON THE OPPOSITE
SIDE of the line as the origin is on, and since the origin is BELOW and
to the LEFT of the GREEN line, the solution set is ABOVE and to the RIGHT
of its boundary line, the GREEN LINE.
,0) and is the GREEN line. Since the origin (0,0) substituted for
(x,y) in the inequality 3x + 1y ≥ 13 gives 0 ≤ 13, which is
FALSE, the solution set for the inequality 1x + 3y ≥ 12 is ON THE OPPOSITE
SIDE of the line as the origin is on, and since the origin is BELOW and
to the LEFT of the GREEN line, the solution set is ABOVE and to the RIGHT
of its boundary line, the GREEN LINE.
 ---
The boundary line for 1x - 1y ≥ 3 has the equation which is
like the inequality but has an equal sign in place of the
inequality symbol. So the boundary line for 1x - 1y ≥ 13 has the
equation 1x - 1y = 3. It has y-intercept (0,3) and x-intercept
(-3,0) and is the BLUE line. Since the origin (0,0) substituted for
(x,y) in the inequality 1x - 1y ≥ 3 gives 0 ≤ 3, which is
FALSE, the solution set for the inequality 1x - 1y ≥ 3 is ON THE OPPOSITE
SIDE of the line as the origin is on, and since the origin is BELOW and
to the LEFT of the BLUE line, the solution set is ABOVE and to the RIGHT
of its boundary line, the BLUE LINE.
So the triangle indicated by
F.R. is the Feasible Region.
---
The boundary line for 1x - 1y ≥ 3 has the equation which is
like the inequality but has an equal sign in place of the
inequality symbol. So the boundary line for 1x - 1y ≥ 13 has the
equation 1x - 1y = 3. It has y-intercept (0,3) and x-intercept
(-3,0) and is the BLUE line. Since the origin (0,0) substituted for
(x,y) in the inequality 1x - 1y ≥ 3 gives 0 ≤ 3, which is
FALSE, the solution set for the inequality 1x - 1y ≥ 3 is ON THE OPPOSITE
SIDE of the line as the origin is on, and since the origin is BELOW and
to the LEFT of the BLUE line, the solution set is ABOVE and to the RIGHT
of its boundary line, the BLUE LINE.
So the triangle indicated by
F.R. is the Feasible Region.
 Now we must find the three corner points (vertices) of the triangle
region
We solve the equations of the red and green lines by substitution
or elimination and get x =
Now we must find the three corner points (vertices) of the triangle
region
We solve the equations of the red and green lines by substitution
or elimination and get x = 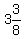 , and y =
, and y = 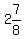 .
That's the point
.
That's the point  We solve the equations of the red and blue lines by substitution
or elimination and get x =
We solve the equations of the red and blue lines by substitution
or elimination and get x = 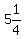 , and y =
, and y =  .
That's the point
.
That's the point 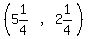 we solve the equations of the blue and green lines by substitution
or elimination and get x = 4, and y = 1.
That's the point (4,1)
Finally we calculate the objective expression 2x + 2y at each of
those corner points:
Substituting x =
we solve the equations of the blue and green lines by substitution
or elimination and get x = 4, and y = 1.
That's the point (4,1)
Finally we calculate the objective expression 2x + 2y at each of
those corner points:
Substituting x = 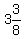 , and y =
, and y = 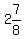 into 2x + 2y gives
into 2x + 2y gives  .
Substituting x =
.
Substituting x = 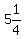 , and y =
, and y =  into 2x + 2y gives 15.
Substituting x = 4, and y = 1 into 2x + 2y gives 10
So the minimum value of 2x + 2y is 10 when x = 4 and y = 1.
Edwin
into 2x + 2y gives 15.
Substituting x = 4, and y = 1 into 2x + 2y gives 10
So the minimum value of 2x + 2y is 10 when x = 4 and y = 1.
Edwin