|
Question 1124980: Graph the system of inequalities
y is greater or equal to x^3 + 5x^2 + 2x - 8
5x - 7y is greater than or equal to -14
x is smaller than or equal to 0
y is smaller than or equal to 0
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the easiest way to graph this is to use the desmos.com calculator.
that can be found at https://www.desmos.com/calculator
when you use this calculator, you graph the opposite of the inequalities.
the area of the graph that is not shaded is your region of feasibility.
the inequalities are:
y >= x^3 + 5x^2 + 2x - 8
5x - 5y >= -14
x <= 0
y <= 0
you would graph the opposite of these inequalities as shown below:
y <= x^3 + 5x^2 + 2x - 8
5x - 5y <= -14
x >= 0
y >= 0
this calculator is so good that you don't even need to solve for y in order to graph the inequalities.
most other calculators can't even graph the inequalities, let alone let you graph the equation in their original form without having to solve for y.
here's the result of my use of this calculator.

there are 2 regions of feasibility.
the corner point of the first region is (-4.122,-1.322)
the area of feasibility would be the area on and underneath the line created by 5x - 7y >= -14 and the area on and above the curve of y = x^3 + 5x^2 + 2x - 8.
that area has to satisfy both those constraints.
the corner points of the second region are (-2,0), (0,0), (0,-8).
that area of feasibility is the area....
on and under the line of y = 0;
on and to the left of the line x = 0;
on and above the curve of y = x^3 + 5x^2 + 2x - 8.
that area has to satisfy all those constraints.
if you solved for y in all those equations but still used the inequality capabilities of the desmos.com calculator, you would have gotten something that looks like this:
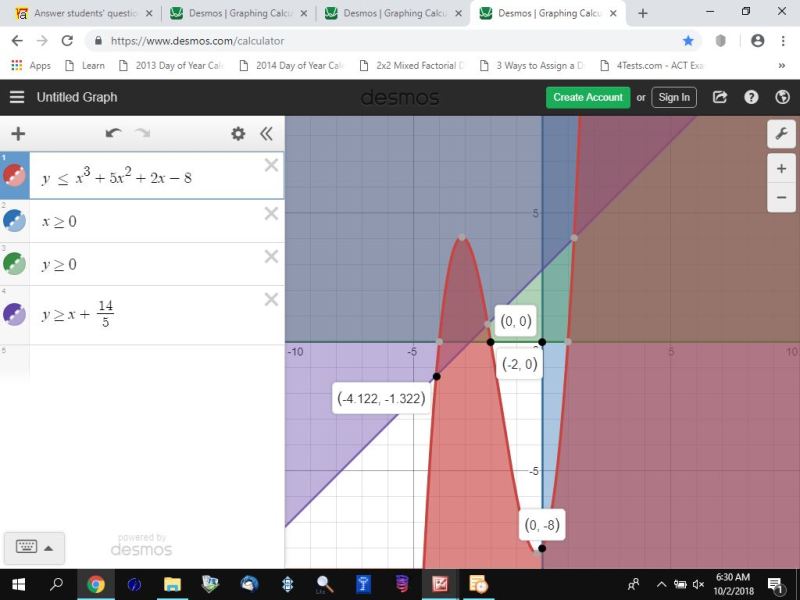
it's the same graph, except that the inequality of 5x - 5y >= -14 becomes y <= x + 14/5 which is then graphed as the inequality of y >= x + 14/5.
if your graphing software doesn't have the ability to graph inequalities, then you would have to graph the equalities and then find the area on the graph that satisfies the inequalities.
your graph would look like this:

you would then have to shade the area of the graph that satisfied all the inequalities.
your graph would look like this:

in this graph, the area that is shaded is the area that satisfied all the inequalities.
those inequalities are, once again:
y >= x^3 + 5x^2 + 2x - 8
5x - 5y >= -14
x <= 0
y <= 0
if you check the inequalities in both those shaded areas, you will see that they satisfy all the constraints.
|
|
|
| |