Question 1124965: On a recent trip, a trucker traveled 325 mi at a constant rate. Because of road conditions, the trucker then reduced the speed by 30 mph. An additional 35 mi was traveled at the reduced rate. The entire trip took 6 h. Find the rate of the trucker for the first 325 mi.
Found 3 solutions by ikleyn, josgarithmetic, greenestamps:
Answer by ikleyn(52879)   (Show Source):
You can put this solution on YOUR website! .
"Time" equation is
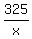 +  = 6 hours.
To solve it, multiply both sides by x*(x-30).
Then simplify and solve the obtained quadratic equation.
Answer. The rate of the tracker under the question is 65 mph.
Answer by josgarithmetic(39630)  (Show Source):
Answer by greenestamps(13209)  (Show Source):
You can put this solution on YOUR website!
The algebraic solutions shown by the other tutors are fine; and you should know the algebraic techniques used in those solutions, so you can use them to solve more complicated problems.
But, if a problem like this does not require a formal algebraic solution, and/or if the speed of finding the solution is important (as in a competitive math contest), then a solution by trial and error is much faster and easier.
The algebraic equation that comes from the given information is
On a competitive exam, the answers are usually "nice" numbers. So look for a value of x that makes "325/x" a whole number less than 6.
325/65 = 5; so x=65 is a good possibility for the answer.
And it works; because then 35/(x-30) = 35/35 = 1, and the sum of the two times is 6 hours.
|
|
|
