.
Let A, B, C and D are the vertices of the trapezoid, so the trapezoid is ABCD.
Let AB be the longer base of 30 cm and CD be the other base of 16 cm long.
Let the point O be the intersection of diagonals.
Then the triangles AOB, BOC, COD and AOD are right angled triangles.
Since the trapezoid ABCD has equal lateral sides, the triangle AOB is isosceles right angled triangle.
Since it base AB is 30 cm long, its sides (the legs) AO and BO are 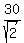 cm long.
Similarly, the triangle COD is isosceles right angled triangle.
Since it base CD is 16 cm long, its sides (the legs) CO and DO are
cm long.
Similarly, the triangle COD is isosceles right angled triangle.
Since it base CD is 16 cm long, its sides (the legs) CO and DO are 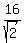 cm long.
Now the areas of the triangles are
for triangle AOB:
cm long.
Now the areas of the triangles are
for triangle AOB: 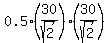 = 225 cm^2;
for triangle COD:
= 225 cm^2;
for triangle COD: 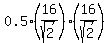 = 64 cm^2;
for triangle BOC:
= 64 cm^2;
for triangle BOC:  = 120 cm^2;
for triangle AOD:
= 120 cm^2;
for triangle AOD:  = 120 cm^2.
The total area of the trapezoid is the sum of areas of triangles 225 + 64 + 120 + 120 = 529 cm^2.
= 120 cm^2.
The total area of the trapezoid is the sum of areas of triangles 225 + 64 + 120 + 120 = 529 cm^2.
Solved.