|
Question 112443: I had a word problem on a test involving Matrices, determinants and Cramer's Rule. I looked through all of my notes, and did not see anything on word problems and the text book was very vague. My professor created the test himself. We were to use a system to solve this word problem:
A boat on a river travels downstream between two points, 20 miles apart, in one hour. The return trip against the current takes 2.5 hours. What is the speed of the current of the river?
My Answer:
x - 20y = 1
x + 20y = 2.5
Using elimination of the y-term 2x = 3.5
x = 3.5/2
Found 2 solutions by Fombitz, bucky:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm confused in your analysis, what is x and what is y?
For these types of problems, start with the following.
Rate x Time = Distance
In your problem, the distance is constant at 20 miles.
When the boat travels downstream, its total rate,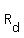 is equal to the rate in still water, is equal to the rate in still water,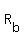 , plus the river rate , plus the river rate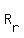 . .
So the equation downstream is
Rate x Time = Distance



When the boat travels upstream, its total rate,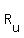 is equal to the rate in still water, is equal to the rate in still water,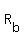 , minus the river rate , minus the river rate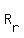 . .
So the equation downstream is
Rate x Time = Distance


 Divide both sides by 2.5. Divide both sides by 2.5.
1.
2.
Adding equation 1 to equation 2 yields,


and from equation 1,
1.


The rate of the boat in still water is 14 mph.
The river moves at a rate of 6 mph.
Hope it helps.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! You had the right idea about finding two equations. The equations you want to use are based
on the relationship:
.
Distance = Rate times Time
.
or
.
D = R * T for short
.
The problem tells you that the Distance the boat travels in one direction is 20 miles. This
is the distance for both equations because the boat travels the same distance each trip. So
substitute 20 for D in the basic equation to get:
.
20 = R * T
.
Going downstream the boat is assisted by the flow of the stream. So the boat travels
at a rate of S + C where S is the speed of the boat in still water and C is the speed of the
current. So we can substitute (S + C) as the true rate of the boat. Also you are told that
for this downstream trip the boat travels 1 hour. So you can substitute 1 for T. These substitutions
make the downstream equation:
.
20 = (S + C)*1 = S + C
.
Transpose the sides to get the more standard form of:
.
S + C = 20
.
We can do the same sort of manipulations for the return trip. This time the current slows
the boat down. So the actual rate of the boat on the return trip is its speed in still water
minus the speed of the current ... or (S - C). And the time of travel for this portion of
the trip is 2.5 hours. Substituting these into the equation 20 = R * T results in:
.
20 = (S - C)*2.5
.
Dividing both sides of this equation by 2.5 gives:
.
8 = S - C
.
and this transposes to:
.
S - C = 8
.
So our two equations (one for each direction) are:
.
S + C = 20
S - C = 8
.
Use Cramer's rule to solve this pair of equations. The denominator determinant is formed from
the coefficients of the unknowns and is:
.
|+1 +1|
|+1 -1|
.
To evaluate this determinant multiply the upper left number (+1) by the lower right number (-1).
This multiplication gives you -1 as the first product.
.
Next, multiply the upper right number (+1) by the lower left number (+1). This product is +1
and this is the second product.
.
The value of the determinant is the difference of the two products ... -1 - (+1) and this
is equal to -2. Remember this result. It is the denominator of the answer.
.
Continuing with Cramer's rule. Since we need to find C we return to the original determinant that
we formed using the coefficients of the unknowns, and we replace the coefficients of
C with the constants on the right side of our two equations. In other words we start with:
.
|+1 +1|
|+1 -1|
.
and replace the right hand column with 20 and 8 as follows:
.
|+1 +20|
|+1 + 8|
.
We evaluate this new determinant the same way as before. First multiply down and to the
right (that is, multiply +1 times +8) and get +8. Next we start with the upper right corner
and multiply down and to the left (that is multiply +20 times +1) and get +20.
.
Then we subtract the second product (+20) from the first product (+8) and get -12.
.
Now we can say that the solution for C is the value of the determinant in which the C column
was replaced with the constants 20 and 8, divided by the value of the first determinant
which was formed from the coefficients of the unknowns S & C. So the value of C is:
.
C = -12/-2 = 6
.
The current C is 6 mph.
.
If you wanted to use Cramer's rule to find S, you would still use the determinant:
.
|+1 +1|
|+1 -1|
.
which has a value of -2 as the denominator. Then you would replace the S column with the
constants 20 and 8 to get the determinant:
.
|+20 +1|
|+ 8 -1|
.
Use the same multiplication pattern, down and to the right (+20 * -1) and down and to the
left (+1 * +8) and subtract to get -20 - 8 = -28 as the value of this determinant.
Divide it by the coefficient determinant which has a value of -2 and you get:
.
S = -28/-2 = 14 mph
.
This tells you that the speed of the boat in still water is 14 mph.
.
This is a quick run-through on 2 by 2 determinants and how to evaluate them. And also a
quick run-through of Cramer's rule. Hope it's not too confusing.
.
|
|
|
| |