Question 1124245: Can you help me to solve and understand this problem. please:
A Ferris wheel 70 feet in diameter completes one revolution every 58 seconds. Its central point is 40 feet above the ground.
a) write a sinusoidal function H(t) to model a rider's height above ground as a fusion of time t in seconds.
b) how long does. it take a rider to go from the lowest point of travel to 61 feet above the ground?
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you spin a radius vector,  , at the origin, , at the origin,
It traces out a sine wave plotted on the time axis.
It has a -r to +r height, so the height is 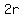
——————
In your problem,  and and 
If the Ferris wheel was at ground level, the
function would be  , ,
but they want the center 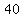 ft above ground, ft above ground,
So the function is: 
——————-
b)
Find 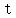 when when 



If this was:
 then, in radians, then, in radians,
 radians ( calculator ) radians ( calculator )
Now I can say:


 sec sec
———————————
Here’s a plot:
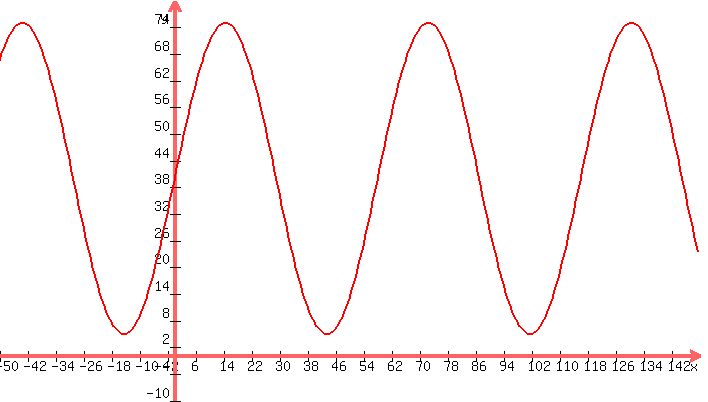
Note that with this curve, you would have to get on
the Ferris wheel at the 58 sec time. If you used -cos instead of
sin, then you get on at the zero time mark
Hope all this helps
|
|
|