SOLUTION: Suppose a triangle with side lengths a,b,c has an in radius r=1, circumradius R=3 and a semiperimeter s=7. Find a^2+b^2+c^2.

1.  Calculate the area of the triangle via  inradius "r" and  semi-perimeter "s" in this way:

        Area = r*s.                                          (1)

    It gives you  Area = 1*7 = 7 square units.



2.  Use the Heron's formula for the area:

        Area = ,    which gives you

        7 = .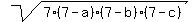


    Square both sides to get

       7^2 = 7*(7-a)*(7-b)*(7-c).


    Cancel the factor 7 in both sides

       7 = (7-a)*(7-b)*(7-c).


       7 = (49 - 7a - 7b + ab)*(7-c) = 

         = 343 - 49a - 49b + 7ab - 49c + 7ac + 7bc - abc = 

         = 343 - 49*(a + b + c) + 7*(ab + bc + ac) - abc.     (2)


3.  You are given the semi-perimeter  s = 7,  so you know the perimeter too:

         a + b + c = 7*2 = 14.                                (3)


    Substitute it into the formula (2) to get

         7 = 343 - 49*14 + 7*(ab + bc + ac) - abc.            (4)


4.  To find abc, use the formula for the area of a triangle 

       Area = ,   where R is the circumradius             (5)


    Substituting the given and known data, it gives you

       7 = ,    or    abc = 7*4*3 = 84.                   (6)


5.  Substitute the found value of abc into (4) to get       

       7 = 343 - 49*14 + 7*(ab + bc + ac) - 84.


    Simplify

       ab + bc + ac = 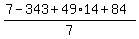 = 62.                   (7)


6.  Now you are in one step from getting the answer.

    You have 

        a + b + c = 14.


    Square it:

        (a + b + c)^2 = 14^2 = 196 = a^2 + b^2 + c^2 + 2*(ab + ac + bc),

    or

        a^2 + b^2 + c^2 = 196 - 2*(ab + ac + bc) = 196 - 2*62 = 72.


Answer.  a^2 + b^2 + c^2 = 72.