Question 1124033: Find k so that (k + 1)x^2 + 5x + 2k - 1 = 0 has two real solutions.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find  so that so that has has   solutions. solutions.
use discriminant:
if discriminant is negative,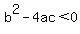 , our equation has two complex solutions , our equation has two complex solutions
if discriminant is positive,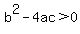 , our equation has , our equation has  solutions which they are real solutions which they are real
if discriminant is zero,  , our equation has one solution which is real , our equation has one solution which is real
 ...here, ...here,  , , , and , and 
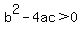
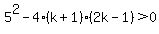
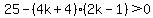
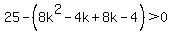

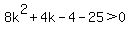
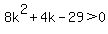
use quadratic formula:





solutions:






so, we will have 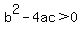 if if  and and 
check:
 ...if ...if 



solutions are:
 ≈ ≈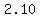
 ≈ ≈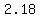
graph:

 ...if ...if 



solutions:
 ≈ ≈
 ≈ ≈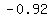

|
|
|