SOLUTION: if u= int (f(sin2x)sinx)dx on [0 ,pi/2] and v= int (f(cos2x)cosx)dx on [0 ,pi/2] then u/v =......

Algebra ->  Graphs -> SOLUTION: if u= int (f(sin2x)sinx)dx on [0 ,pi/2] and v= int (f(cos2x)cosx)dx on [0 ,pi/2] then u/v =......      Log On


   

Question 1123840: if u= int (f(sin2x)sinx)dx on [0 ,pi/2] and v= int (f(cos2x)cosx)dx on [0 ,pi/2]
then u/v =......
Answer by ikleyn(52855) About Me  (Show Source):
You can put this solution on YOUR website!
.

In order for the problem makes sense, it should be written in this precise form 

    if u= int (f(sin^2(x))sinx)dx on [0 ,pi/2] and v= int (f(cos^2(x))cosx)dx on [0 ,pi/2]
 then u/v =......

Solution 

Use the change of variables



    u = int (f(sin^2(x))sinx)dx on [0 ,pi/2] = int (-f(sin^2(x))d(cos(x)) on [0 ,pi/2] = int (-f(1-cos^2(x))d(cos(x)) on [0 ,pi/2] =

      = -int (f(1-t^2)dt  on [1,0]  (where t = cos(x) );



    v = int (f(cos^2(x))cosx)dx [0 ,pi/2] = int (f(cos^2(x))d(sin(x))dx [0 ,pi/2] = int (f(1-sin^2(x))d(sin(x))dx [0 ,pi/2] = 

      = int (f(1-t^2)dt on [0,1]  (where t = sin(x) ).



   Since  -int (f(1-t^2)dt  on [1,0] = int (f(1-t^2)dt on [0,1],  we have 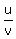 u%2Fv = 1.

Solved.