Question 1123804: At the festival, you are selling hats and T-shirts. In total you sell 140 hats and t-shirts combined. Each hat costs $10 and each shirt costs $15. Your profit from selling the shirts is $1800 dollars. How many hats did you sell? How many t-shirts?
Found 3 solutions by ikleyn, josgarithmetic, MathTherapy:
Answer by ikleyn(52750)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. You can setup the problem as the system of 2 equations in 2 unknowns.
H + T = 140 (1) (counting items) (H stands for hats; T stands for T-shirts)
10H + 15T = 1800 dollars (2) (counting dollars, i.e. revenue)
Solve it using the Substitution method. For it, express H = 140-T from eq(1) and then substitute it into eq(2).
10*(140-T) + 15T = 1800 (3)
10*140 - 10T + 15T = 1800
(15-10)T = 1800 - 10*140
T = 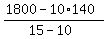 = 80.
Answer. 80 T-shirts and 140-80 = 60 hats.
Check. 10*60 + 15*80 = 1800 dollars. ! Correct ! = 80.
Answer. 80 T-shirts and 140-80 = 60 hats.
Check. 10*60 + 15*80 = 1800 dollars. ! Correct !
2. Another way to setup is to use only one equation for one unknown from the very beginning.
Let T be the number of T-shirts.
Then the number of hats is 140-T, according to the condition.
The revenue equation is
15*T + 10*(140-T) = 1800 dollars.
It is the same equation as equation (3) above.
Solve it by the same method.
Surely, you will get the same answer.
3. There is the third way to solve it - without using any equations.
It is ONE LINE solution
T = 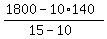 = 80 T-shirts. = 80 T-shirts.
I will explain you now how to write/(how to derive on the way) this ONE LINE formula and solution without using equations.
Let assume for a minute that all 140 sold items were hats.
Then the revenue would be 10*140 dollars, making shortage of 1800 - 10*140 dollars comparing with the real revenue.
The shortage is due to the fact that we counted all items at 10 dollars each.
To compensate the difference, we should to replace back some number of hats by T-shirts in our calculations.
At each such replacement, we diminish the difference of 1800-10*140 dollars by (15-10) dollars.
It is clear that the number of such replacements is the ratio 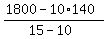 , exactly the ratio in the ONE LINE solution formula (!).
Now it is easy to calculate , exactly the ratio in the ONE LINE solution formula (!).
Now it is easy to calculate 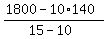 = 80 -shirts by obtaining the same answer as above.
Using this logic, you can write the solution of any similar problem in ONE LINE without using any equation.
The logic, which you just learned, will keep you on the right track and will always help you to write this formula correctly. = 80 -shirts by obtaining the same answer as above.
Using this logic, you can write the solution of any similar problem in ONE LINE without using any equation.
The logic, which you just learned, will keep you on the right track and will always help you to write this formula correctly.
-------------------
Congratulations ! Now you are familiar with 3 basic methods for the given problem.
I suggest that algebraic methods will be your basic methods for such problems,
and the logical analysis method will allow you to solve the problems MENTALLY without using equations.
I will be happy if it will make your horizon wider.
--------------
To see other similar problems solved by the same methods, look into the lesson
- Three methods for solving standard (typical) problems on tickets
in this site.
To see how the logical method works for other similar problems, look into the lessons
- Problem on two-wheel and three-wheel bicycles
- Problem on animals at a farm
- Problem on pills in containers
- What type of problems are these?
in this site.
Answer by josgarithmetic(39613)   (Show Source): (Show Source):
You can put this solution on YOUR website! h hats
t tee-shirts

-
cost, 
But what kind of cost was this? Prices for selling at the festival used, or prices for you to first purchase the items before YOU sell them at festival?
1800 dollars profit?
What about revenue?
INCOMPLETE PROBLEM DESCRIPTION
Answer by MathTherapy(10549)   (Show Source): (Show Source):
You can put this solution on YOUR website!
At the festival, you are selling hats and T-shirts. In total you sell 140 hats and t-shirts combined. Each hat costs $10 and each shirt costs $15. Your profit from selling the shirts is $1800 dollars. How many hats did you sell? How many t-shirts?
NOT profit, but REVENUE from sales = $1,800
Let number of t-shirts be T
Then number of hats = 140 - T
We then get: 15T + 10(140 - T) = 1,800
15T + 1,400 - 10T = 1,800
15T - 10T = 1,800 - 1,400
5T = 400
T, or number of t-shirts = 
Number of hats: 
|
|
|