Question 1123725: APEX Company produces and sells three products: X, Y and Z. In order to produce them, the company needs to purchase four raw materials A, B, C and D. The prices of these four raw materials are $15/kg, $20/kg, $25/kg and $10/kg, respectively. Each month, the company has a limited budget of $50,000 to buy the raw materials. Producing one X requires 200g of A, 500g of C and 400g of D. Producing one Y requires 500g of A, 800g of B and 700g of C. Producing one Z requires 200g of A, 300g of B, 300g of C and 400g of D. The selling price of each product is based on the cost of raw materials: the profit margins of X, Y, and Z are 20%, 10%, and 25%, respectively.
From past historical data, the manager knows that due to economic situation, the monthly production of X and Z should be capped at 500 and 400 respectively. Besides, the monthly production of Y should be less than two third of the sum of the monthly production of X, Y and Z. Moreover, the monthly production of each product should be at least 100.
(a) Based on the given scenario above, develop a linear programming model to determine the optimal amount of products that the company should produce each month so that its profit is maximized. State your own assumptions and write the objective function and constraints clearly. (10 marks)
(b) Use Excel solver to solve the problem. Note down Answer Report and Sensitivity Report. Based on the report(s), identify the optimal solution and explain which constraints are binding and which are not. (5 marks)
(c) Interpret the sensitivity report from solver and discuss the following scenarios (without re-solving it using Excel Solver). (i) If the monthly budget available is $80,000, how does it affect the optimal profit? If the monthly budget available is $30,000, how does it affect the optimal profit? (4 marks)
(ii) If the profit margin of Y becomes 15% and the profit margin of X becomes 12%, is there a change in the optimal solution? (4 marks)
(d) Discuss how changes in the budget and the selling prices will affect the company’s decisions and profit. (Hint: you need to consider demand.) (12 marks)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let x = the number of product X that are sold.
let y = the number of product Y that are sold.
let z = the number of product Z that are sold.
create a unit cost for product X, Y, Z based on the quantities of each type of raw material (A, B, C, D) multiplied by the cost per gram.
the costs given were costs per kilogram, so they needed to be divided by 1000 to get the cost per gram.
this was necessary since the quantities of material were in grams.
the table shown in excel columns C through G, rows 3 through 7 was used to create the unit costs for product X, Y, Z shown in column C through F, row 7.
once those unit costs were developed, then the constraint equations could be created.
an example of the creation of a unit cost is as follows;
product X has 200 grams of material A, 0 grams of material B, 500 grams of material C, 400 grams of material D.
the cost per kilogram for material A is 15; for material B is 20; for material C is 25; for material D is 10.
the cost per kilogram is divided by 100 to get the cost per gram.
.015 for material A; .020 for material B; .025 for material C; .010 for material D.
the unit cost for product X is equal to:
200 * .015 + 0 * .020 + 500 * .025 + 400 * .010 = 19.5.
the unit costs for each product are shown in the excel spreadsheet in columns C through F, row 7.
the total cost for product X would be the number of units of product X times the unit cost for product X.
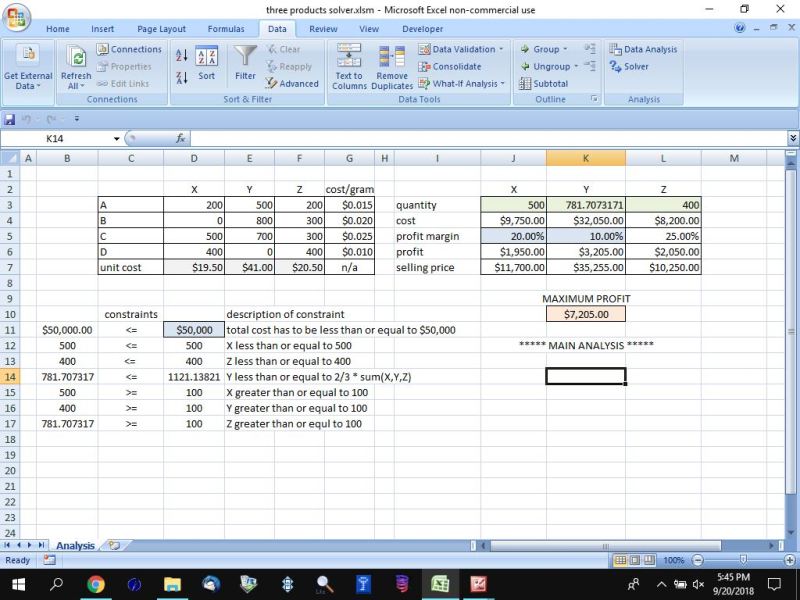
in the main analysis, the total cost for product X becomes $9.750.
this is based on 500 * 19.5 = 9750.
the number of units for product X is in cell J3 (column J row 3).
the total cost for product X in cell J4.
the unit cost for product X is in cell D7.
the profit margin for each product is in cells J5, K5, L5
the objective function is:
profit = profit margin * total cost for product X plus profit margin * total cost for product Y plus profit margin * total cost for product Z.
in the main analysis, this becomes:
profit = .2 * 9750 + .1 * 32050 + .25 * 8200 = 7205.
in the excel spreadsheet for the main analysis, this would be cell J4 * J5 + K4 * K5 + L4 * L5 with the results being stored in cell K10.
for the main analysis, the constraint functions are:
total cost is less than or equal to $50,000.
units of product X are less than or equal to 500.
units of product Z are less than or equal to 400.
units of product Y are less than or equal to 2/3 * sum of units for (product X, product Y, product Z).
units of product X are greater than or equal to 100.
units of product Y are greater than or equal to 100.
units of product Z are greater than or equal to 100.
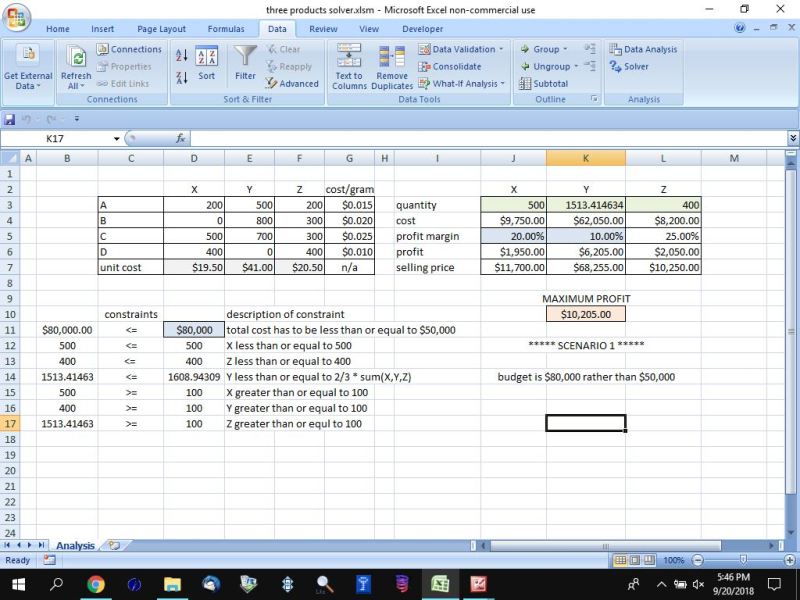
for scenario 1 analysis, everything is the same except the total cost is less than or equal to $80,000.
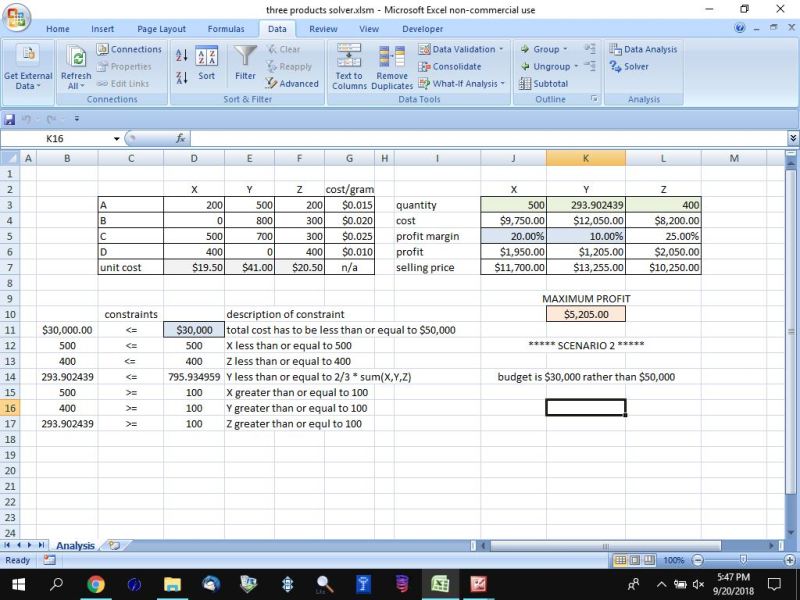
for scenario 2 analysis, everything is the same except the total cost if less than or equal to $30,000.
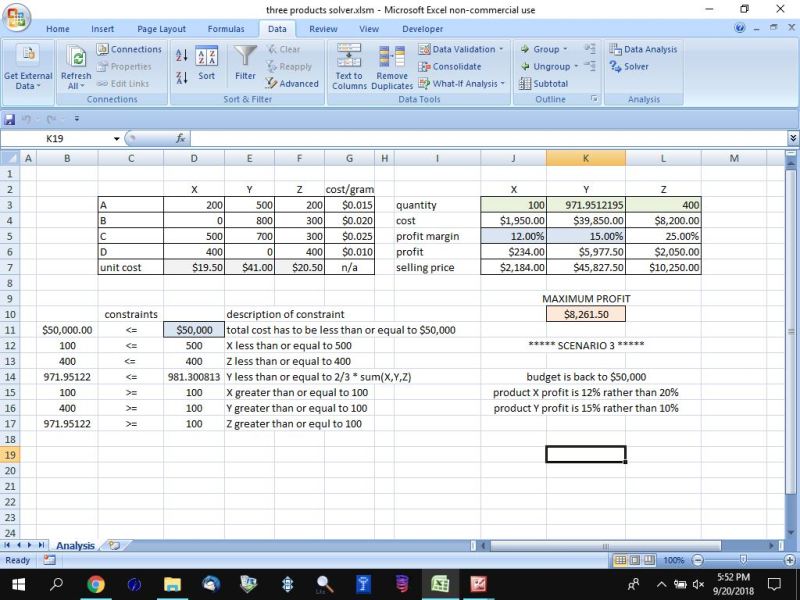
for scenario 3 analysis, everything is the same except the total cost is back to less than or equal to $50,000 and the profit margin for product X is 12% instead of 20% and the profit margin for product Y is 15% rather than 10%.
the main analysis is shown below:
scenario 1 analysis is shown below:
scenario 2 analysis is shown below:
scenario 3 analysis is shown below:
the main analysis reports are shown below:
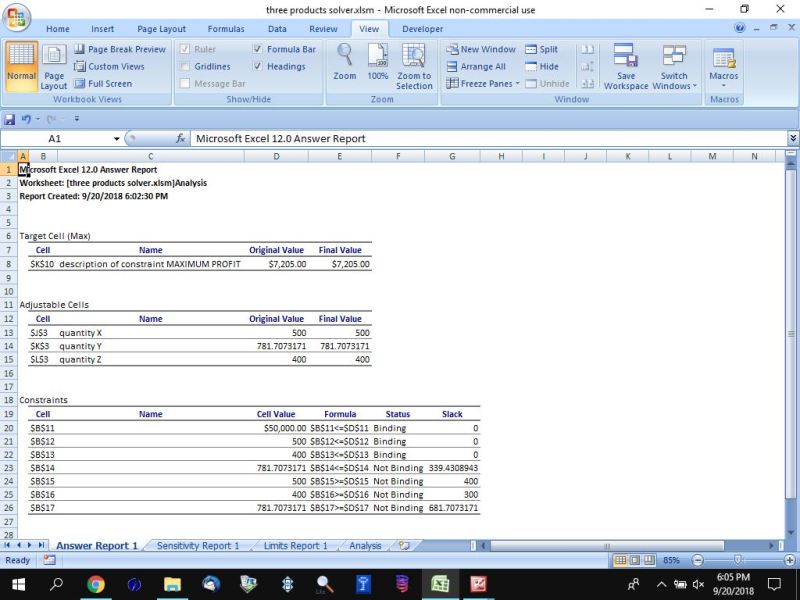
Answer Report:
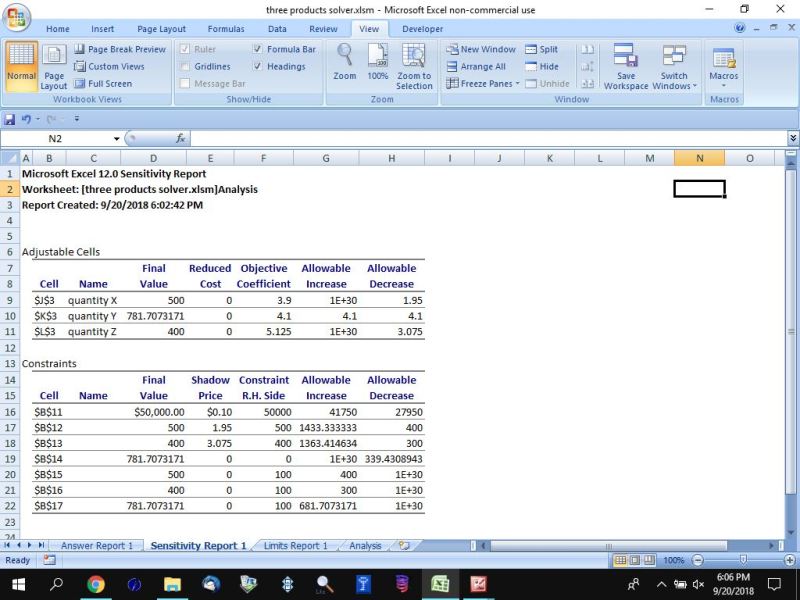
Sensitivity Report:
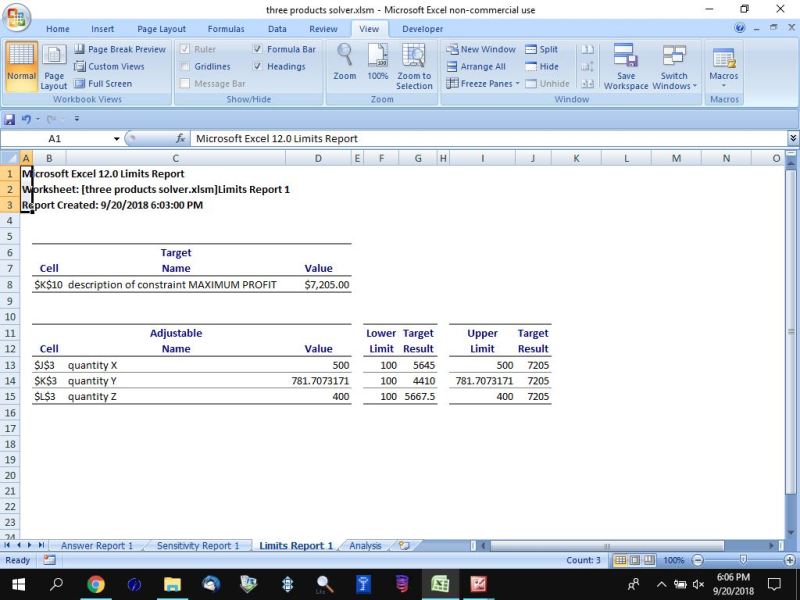
Limits Report:
answers to your questions to the best of my knowledge are shown below:
------------------------------------------------
(a) Based on the given scenario above, develop a linear programming model to determine the optimal amount of products that the company should produce each month so that its profit is maximized. State your own assumptions and write the objective function and constraints clearly. (10 marks)
done above.
if you have any questions or need further clarification send me an email and i'll answer as best i can.
(b) Use Excel solver to solve the problem. Note down Answer Report and Sensitivity Report. Based on the report(s), identify the optimal solution and explain which constraints are binding and which are not. (5 marks)
see the excel printout for the main analysis.
also see the reports shown below.
a binding requirement is one that has no more room to grow.
looking at the answer report, it turns out that the requirements that are binding are:
budget in cell B11.
number of units of product X in bell B12.
number of units of product Z in cell B13.
these are binding because they are at their maximum allowed limits.
number of units of product Y in cell B14 is not binding because it still has room to grow.
(c) Interpret the sensitivity report from solver and discuss the following scenarios (without re-solving it using Excel Solver). (i) If the monthly budget available is $80,000, how does it affect the optimal profit? If the monthly budget available is $30,000, how does it affect the optimal profit? (4 marks)
if the budget is increased to $80,000, the maximum profit will get larger because there will be more units of product Y.
the number of units of product X and Z are not affected because they are already at their maximum allowable limit.
product Y does have a maximum number of units as well but it hasn't reached that yet.
the absolute maximum for product Y is 1800 units based on the formula for determining the maximum allowable units for product Y,.
the formula for determining the maximum number of units of product Y is:
y <= 2/3 * (x + y + z)
x,y,z are number of units for product X, Y, Z.
simplify this formula to get:
y <= 2/3 * x + 2/3 * y + 2/3 * z
subtract 2/3 * y from both sides of this equation to get:
y - 2/3 * y <= 2/3 * x + 2/3 * z
simplify to get:
1/3 * y = 2/3 * x + 2/3 * z
multiply both sides of this equation by 3 to get:
y <= 2 * x + 2 * z
factor to get:
y <= 2 * (x + z)
since x + z can go no higher than 900, this becomes:
y <= 1800.
the value of y can't go higher than 1800 as long as the limits on x and z remain at 500 and 400 respectively.
i did an analysis with a much higher budget and confirmed that the number of units of product Y will never go higher than 1800 as long as the number of units of product X and Z remains at the 900 limit.
(ii) If the profit margin of Y becomes 15% and the profit margin of X becomes 12%, is there a change in the optimal solution? (4 marks)
in the main analysis, the profit margins of product X and Z are higher than the profit margin of product Y.
it stands to reason that the algorithm will maximize the number of units of product X and Z before adding units of product Y.
when the profit margin of product X is made than the profit margin of product Y, the situation reverses and product Y is selected in preference to product X.
number of units of product X drops to 100 and number of units of product Y jumps to 971.9.....
the only thing that stops the number of units of product X to go below 100 is because there is a constraint that tells the algorithm that the number of units of product X can't go below 100.
(d) Discuss how changes in the budget and the selling prices will affect the company’s decisions and profit. (Hint: you need to consider demand.) (12 marks)
it is clear that the budget is a constraining factor.
the higher the budget, the more units of product X, Y, Z that can be sold.
this continue up to the maximum number of units of each product that can be sold.
that would be 500 for product X, 400 for product Z and 1800 for product Y as explained above.
the more units sold, the more revenue, which results in more profit.
if the selling price goes up, then each unit sold will generate more profit.
there is a limiting factor, however.
the demand is bawed on the selling price.
make the selling price too high and the demand goes down.
this means that there is probably a limit on the profit that can be made based on the fact that higher price creates less demand and lower price creates higher demand.
there are other factors as well, such as whether the product is a necessary product or a desirable product.
a necessary product will continue with demand despite higher prices more than a desirable product that is non-essential.
it looks to me like you are free to bring up more than just what's in the problem statement when discussing the impact on profit.
that i'll leave up to you.
i don't know what else i can tell you.
i'm available if you have questions regarding this material.
i also have the excel spreadsheet which i can send to you once i know your email address.
|
|
|