Question 1123590: a plane travels 390 miles in 2 hours traveling with the wind, going against the wind, the plane travels 330 mile in the same time. find the speed of the plane in still air and the speed of the wind.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The effective speed of the plane traveling with the wind is 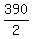 = 195 miles per hour.
It is equal to the sum of the plane speed u "in still air" plus the speed of the wind v:
u + v = 195. (1)
It is your first equation.
The effective speed of the plane traveling against the wind is = 195 miles per hour.
It is equal to the sum of the plane speed u "in still air" plus the speed of the wind v:
u + v = 195. (1)
It is your first equation.
The effective speed of the plane traveling against the wind is 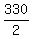 = 165 miles per hour, according to the condition.
It is equal to the difference of the plane speed u "in still air" minus the speed of the wind v:
u - v = 165. (2)
It is your second equation.
So you have this system of two equations:
u + v = 195 (1)
u - v = 165 (2)
The easy way to solve it is to add the two equations. When you add them, the terms "v" and "-v" cancel each other,
and you get a single equation for the unknown u
2u = 195 + 165 = 360,
which implies
u = 360/2 = 180 miles per hour.
Thus you just found the speed of the plane at no wind.
The last step is to find v from equation (1):
v = 195 - 180 = 15 miles per hour.
Answer. The speed of the plane in still air is 180 mph.
The speed of the wind is 15 mph. = 165 miles per hour, according to the condition.
It is equal to the difference of the plane speed u "in still air" minus the speed of the wind v:
u - v = 165. (2)
It is your second equation.
So you have this system of two equations:
u + v = 195 (1)
u - v = 165 (2)
The easy way to solve it is to add the two equations. When you add them, the terms "v" and "-v" cancel each other,
and you get a single equation for the unknown u
2u = 195 + 165 = 360,
which implies
u = 360/2 = 180 miles per hour.
Thus you just found the speed of the plane at no wind.
The last step is to find v from equation (1):
v = 195 - 180 = 15 miles per hour.
Answer. The speed of the plane in still air is 180 mph.
The speed of the wind is 15 mph.
Solved.
The method which I used to solve the system (1), (2) is called the Elimination method.
----------------
To see many other similar solved problems, look into the lessons
- Wind and Current problems
- Wind and Current problems solvable by quadratic equations
- Selected problems from the archive on a plane flying with and against the wind
in this site, where you will find other similar solved problems with detailed explanations.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn shows a perfectly good method for solving the problem, finding the average speed with the wind and the average speed against the wind; then using algebra to set up two equations involving the plane's speed and the wind speed and solving them.
If the method of solving the problem is not specified, and in particular if the speed of solving a problem is important (as in a competitive exam), then here is another way to get from the two average speeds without algebra, using logical analysis and just a bit of simple arithmetic.
Think of the speeds on a number line. The speed of the plane is some number; if you add the speed of the wind, you get to some higher number, and if you subtract the speed of the wind, you get to some lower number.
Since you went the same distance in each direction to get to those other numbers, the speed of the plane is halfway between those two numbers.
So in this problem we have the two average speeds, with and against the wind, as 195 and 165 mph. The speed of the plane is halfway between those two speeds: 180 mph. Then the speed of the wind is how far 165 and 195 are away from 180, which is 15.
Without all the words of explanation, here is the solution process:
(1) average speed with the wind: 390/2 = 195
(2) average speed against the wind: 330/2 = 165
(3) plane speed: (195+165)/2 = 180 [halfway between 195 and 165; or average of 195 and 165]
(4) wind speed: 195-180 = 15, or 180-165 = 15
The computations with this method are exactly the computations you do using algebra; you just save the time of writing down the system of equations and solving them.
|
|
|