SOLUTION: If Team A and Team B work together, they can finish a project in 6 days. Team A is twice as efficient as Team B. How long does it take for each team to finish the project individua

Let R be rate of work of the team B.  (= the part of job the team B complete dayli).


Then the rate of work of the team A is twice of it, i.e. 2R


From the condition, we have 


    2R + R =      <<<---=== it is exactly what the condition says about two reams A and B working together.


This equation is  3R = ,  or, equivalently,  R = 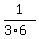 = ,  which exactly means that the team B will complete the job in 18 days.


Then you may conclude that the team A will complete the job in 18/2 = 9 days.

Team A works as two teams B.


Since A + B  complete the job in 6 days, it means that three teams B working together will complete the job in 6 days.


Hence, one single team B will complete the job in 3*6 = 18 days working alone.


Then the Team A will complete it in 9 days working alone.


Check.   +  =  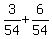=  = .   ! Correct !