SOLUTION: The Alpha Furniture Company manufactures dining room tables and chairs. Each table requires 50 board feet and 3 hours of labor. Each chair takes 20 board feet and 4 hours of labor.

Let X be the number of tables;

let Y be the number of chairs.


The objective function (profit)  is

R(X,Y) = 200X + 100Y.


The restrictions are :

50X + 20Y <= 3300       (1)     (restriction on board feet of lumber)   and
 3X +  4Y <=  380       (2)     (restriction on labor time).
X >= 0;  Y >= 0.        (3)     (non-negativity).


You need to maximize the objective function (profit) under given restrictions.


The feasible domain is shown below.


It is  a quadrilateral in the first quadrant  (X >= 0,  Y >= 0)  restricted 
by the red line  50X + 20Y = 3300  and the green line  3X + 4Y = 380.






Plots Y = 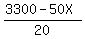  (red) and y =  (green)



The method of linear programming says:

    1) Take the vertices of this quadrilateral

        (X1,Y1) = (0,95)    (green line Y-intercept);

        (X2,Y2) = (40,65)   (intersection point of the straight lines 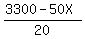Y =  and Y =  );
        (X3,Y3) = (66,0)    (red line X-intercept)


    2) Calculate the objective function at these points

        R(X1,Y1) = 200*0 + 100*95   =  9500;

        R(X2,Y2) = 200*40 + 100*65  =  14500;

        R(X3,Y3) = 200*66 + 100*0   =  13200.


    3) Then select one of these points where the objective function is maximal - In our case this point is (X2,Y2) = (40,65).


    4) This point gives your optimal solution X = 40 tables  and Y = 65 chairs.


If they follow this optimal solution, their profit will be MAXIMAL, $14500.