|
Question 1123191: The sum of the reciprocals of two real numbers is -1, and the sum of their cubes is 4, What are the numbers?
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
 + +  = -1, (1) = -1, (1)
 + +  = 4. (2)
From (1), you have x + y = -xy. (3)
Equation (2) you can transform in this way = 4. (2)
From (1), you have x + y = -xy. (3)
Equation (2) you can transform in this way
 = {{(x+y)*(x^2 - xy + y^2)}}} = = {{(x+y)*(x^2 - xy + y^2)}}} = 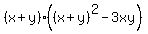 = 4. (4)
In equation (4), replace (x+y) by -xy, based on (3). You will get
(-xy)*((-xy)^2 - 3xy) = 4. (5)
Introduce new variable t = xy. Then equation (5) takes the form
(-t)*((-t)^2 - 3t) = 4, or
-t*(t^2 - 3t) = 4, which is reduced to
t^3 - 3t^2 - 4 = 0. (6)
Notice that equation (5) has the root t= -1 (you can check it directly).
Hence, the binomial (t+1) divides the polynomial in the left side of (6) without a remainder.
Making a long division, you get
t^3 - 3t^2 - 4 = (t+1)*(t^2 -4t+4) = (t-1)*(t-2)^2.
Thus the equation (6) has two real roots: a) t= -1 of the multiplicity 1 and b) t= 2 of the multiplicity (2).
Now we must consider two cases.
Case 1. t= -1. Then xy = -1 due to definition of t, and we have this system of 2 equations
x + y = -xy = 1 (7), (due to (3)) and
xy = -1. (8)
Again
x + y = 1 (7) and
xy = -1.
By substitution y = 1-x, it is reduced to the quadratic equation
x(1-x) = -1 ====> x^2 - x -1 = 0 with the roots = 4. (4)
In equation (4), replace (x+y) by -xy, based on (3). You will get
(-xy)*((-xy)^2 - 3xy) = 4. (5)
Introduce new variable t = xy. Then equation (5) takes the form
(-t)*((-t)^2 - 3t) = 4, or
-t*(t^2 - 3t) = 4, which is reduced to
t^3 - 3t^2 - 4 = 0. (6)
Notice that equation (5) has the root t= -1 (you can check it directly).
Hence, the binomial (t+1) divides the polynomial in the left side of (6) without a remainder.
Making a long division, you get
t^3 - 3t^2 - 4 = (t+1)*(t^2 -4t+4) = (t-1)*(t-2)^2.
Thus the equation (6) has two real roots: a) t= -1 of the multiplicity 1 and b) t= 2 of the multiplicity (2).
Now we must consider two cases.
Case 1. t= -1. Then xy = -1 due to definition of t, and we have this system of 2 equations
x + y = -xy = 1 (7), (due to (3)) and
xy = -1. (8)
Again
x + y = 1 (7) and
xy = -1.
By substitution y = 1-x, it is reduced to the quadratic equation
x(1-x) = -1 ====> x^2 - x -1 = 0 with the roots  = =  .
So this case produces the pair of solutions
x = .
So this case produces the pair of solutions
x = 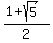 , y = 1-x = , y = 1-x = 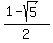 and
x = and
x = 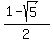 , y = 1-x = , y = 1-x = 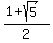 .
Case 1 is completed.
Case 2. t= 2. Then xy = 2 due to definition of t, and we have this system of 2 equations
x + y = -xy = -2 (9), (due to (3)) and
xy = 2. (10)
By substitution y = -2-x, it is reduced to the quadratic equation
x(-2-x) = 2 ====> x^2 - 2x +2 = 0, which has no real solutions.
Case 2 is completed, too.
Thus we get the ANSWER : The given system has the pair of real solutions
x = .
Case 1 is completed.
Case 2. t= 2. Then xy = 2 due to definition of t, and we have this system of 2 equations
x + y = -xy = -2 (9), (due to (3)) and
xy = 2. (10)
By substitution y = -2-x, it is reduced to the quadratic equation
x(-2-x) = 2 ====> x^2 - 2x +2 = 0, which has no real solutions.
Case 2 is completed, too.
Thus we get the ANSWER : The given system has the pair of real solutions
x = 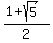 , y = 1-x = , y = 1-x = 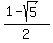 and
x = and
x = 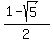 , y = 1-x = , y = 1-x = 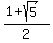 . .
Solved.
|
|
|
| |