|
Question 1123011: If the second of three consecutive integers is subtracted from 147 the result is the first and third what are the integers
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39625)   (Show Source):
Answer by ikleyn(52847)  (Show Source):
You can put this solution on YOUR website! .
If the second of three consecutive integers is subtracted from 147 the result is the  of the first and the third.
What are the integers ?
~~~~~~~~~~~~~~~~~~
Notice how I edited your post in order for it makes sense.
Let n be the middle of the three consecutive integers.
The the three integers are (n-1), n and (n+1).
The sum of the first and the third integers is (n-1) + (n+1) = 2n.
The condition says
147 - n = 2n.
It is easy to solve:
147 = 3n ====> n = 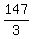 = 49.
Answer. The integers are 48, 49 and 50.
Solved.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Let the three numbers be a, b, and c. (At this point, we don't care that they are consecutive integers.)
The given condition is equivalent to saying that the sum of the three numbers is 147.
That means the average of the three numbers is 147/3 = 49.
Then, since the numbers are three consecutive integers, 49 is the middle one, and the three numbers are 48, 49, and 50.
|
|
|
| |
