Question 1122922: Six hundred people attended the premiere of a motion picture. Adult tickets cost $10, and children were admitted for $3. If box office receipts totaled $2430, how many children attended the premiere?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One line solution
# of adult tickets = 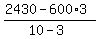 = 90. (*) = 90. (*)
# of children tickets = the rest 600-90 = 510.
Check. 3*510 + 10*90 = 2430 dollars. ! Correct !
Explanation
Let assume for a minute that all 600 visitors were children.
Then the revenue would be 600*3 = 1800 dollars, making the shortage of 2430 - 600*3 dollars, comparing with the real (given) revenue.
It is because we assumed that all tickets were at 3 dollars.
Now we should replace back some number of $3 tickets by $10 tickets.
At each such replacement, we diminish the shortage by 10-3 = 7 dollars.
So, the number of replacements is expressed exactly by the formula (*), which I used in my one line solution above.
And the number of replacements is nothing else as the number of adult tickets.
Solved.
-------------------
An alternative way of solution is to reduce the problem to the system of two equations with two unknowns
or to a single equation for one unknown.
Independently of the method, you will get the same result.
Interesting, that if you apply the determinant method of solution to the system of two equations, you will get THE SAME FORMULA (*) (!)
====================
See the lessons
- Using systems of equations to solve problems on tickets
- Three methods for solving standard (typical) problems on tickets
in this site.
|
|
|